Производная вещественной функции

5.1. Определение. Пусть f - вещественная функция, определенная на [а, b]. Взяв произвольное число х∈[а, b], составим отношение

(1)

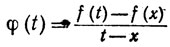
(a<t<b, t≠x)

и положим

(2)

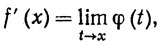
если этот предел существует, в соответствии с определением 4.1.

Таким образом, с функцией f связана функция f', область определения которой - множество всех точек х, в которых существует предел (2); функция f' называется производной функции f.

Если производная f' определена в точке x, то мы будем говорить, что функция f дифференцируема в точке х. Если f' определена в каждой точке некоторого множества E⊂[a, b], то мы будем говорить, что f дифференцируема на Е.

В формуле (2) можно брать правосторонний или левосторонний предел; это приводит к определению правосторонней и левосторонней производной. В частности, в концах сегмента а и Ь производная (если она существует) всегда является соответственно правосторонней и левосторонней. Мы, однако, не будем подробно рассматривать такие производные.

Если f определена на интервале (а, b) и если а<х<b, то f'(х) определяется равенствами (1) и (2), как выше. Но f'(а) и f'(b) в этом случае не определены.

5.2. Теорема.Пусть функция f определена на сегменте [а, b]. Если f дифференцируема в точке х∈[а, b], то она непрерывна в этой точке.

Доказательство. По теореме 4.4 при t→х мы имеем

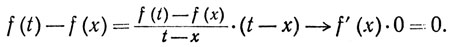
Теорема, обратная к только что доказанной, неверна. Легко построить непрерывные функции, не дифференцируемые в изолированных точках. В гл. 7 мы познакомимся даже с такой функцией, которая, будучи непрерывной на всей прямой, не дифференцируема ни в одной точке!

5.3. Теорема. Пусть f и g определены на [а, b] и дифференцируемы в точке х∈[а, b]. Тогда f+g, fg и f/g дифференцируемы в точке х и

(c)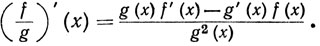

В утверждении (с) мы, разумеется, предполагаем, что g(x)≠0.

Доказательство. Утверждение (а) следует из теоремы 4.4. Пусть h = fg. Тогда

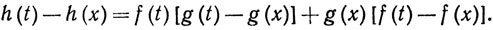
Если мы разделим это равенство на t-x и заметим, что f(t)→f(x) при t→x (теорема 5.2), то получим (6). Наконец, пусть h = f/g. Тогда

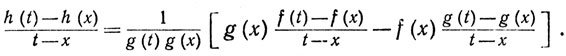
Устремляя t к x и применяя теоремы 4.4 и 5.2, мы получаем (с).

5.4. Примеры. Производная каждой постоянной функции равна, очевидно, нулю. Если f определена равенством f(x) = x, то f'(x) = 1. Повторное применение утверждений (b) и (с) последней теоремы показывает, что функция хⁿ дифференцируема и что ее производная равна nx^n-1, каково бы ни было целое n (если n<0, то мы должны ограничиться точками х≠). Таким образом, любой многочлен дифференцируем. То же верно в отношении любой рациональной функции, если исключить точки, в которых обращается в нуль ее знаменатель.

Следующая теорема дает правило дифференцирования сложной функции. Более общий ее вариант встретится нам в гл. 9.

5.5. Теорема.Пусть f непрерывна на [a, b], f(х) существует в некоторой точке х∈[а, b], g определена на сегменте I, содержащем множество значений функции f, и g дифференцируема в точке f(x). Если

Доказательство. Пусть y = f(x). По определению производной имеем

(4)

(5)

где t∈[a, b], s&38712;I и u(t)→0 при t→x, v(s)→0 при s→y. Пусть s = f(t). Используя сначала (5), а затем (4), получим

или, если t≠х,

(6)

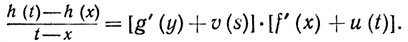
Устремляя t к х, мы видим, что, в силу непрерывности функции f, s→у, поэтому правая часть равенства (6) стремится к g'(y)f'(x), откуда и следует (3).

5.6. Примеры.(а) Пусть функция f определена равенством

(7)

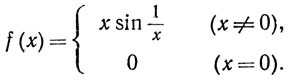
Будем считать доказанным, что производная функции sinx равна cosx (мы будем рассматривать тригонометрические функции в гл. 8). Тогда мы можем применить теоремы 5.3 и 5.5, если х≠0, и получить

(8)

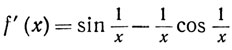
В точке x = 0 эти теоремы уже не применимы, так как дробь ¹/_х там не определена, и мы сошлемся непосредственно на определение: при t≠0

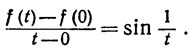
При t→0 это отношение не стремится ни к какому пределу, так что f'(0) не существует.

(b) Пусть функция f определена равенствами

(9)

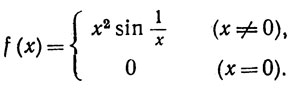
Как и выше, мы получаем

(10)

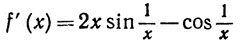
При x = 0 мы вспомним определение и получим

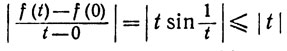
полагая t→0, мы видим, что

Таким образом, функция f дифференцируема во всех точках х, но f не является непрерывной функцией, так как cos(¹/_x) в (10) не стремится ни к какому пределу при х→0.