Бесконечные пределы и пределы в бесконечности

Чтобы иметь возможность действовать в расширенной системе вещественных чисел, мы расширим рамки определения 4.1, сформулировав его в терминах окрестностей.

Для любого вещественного числа х мы уже определили окрестность х как любой интервал вида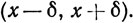

4.32. Определение. При любом вещественном с множество всех вещественных чисел х, таких, что х>с, называется окрестностью точки -∞ и обозначается (с, +∞). Аналогично, множество (-∞, с) называется окрестностью точки -∞.

4.33. Определение. Пусть вещественная функция f определена на множестве Е. Мы будем говорить, что

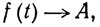
при t→x,

где A и х принадлежат расширенной системе вещественных чисел, если для любой окрестности U точки А существует окрестность V точки x, такая, что множество V∩E непусто и f(t)∈U при всех t∈V∩E, t≠х.

Несложное рассуждение показывает, что это определение совпадает с определением 4.1, когда A и х вещественны.

Аналог теоремы 4.4 справедлив и в том случае, и в его доказательстве не появляется ничего нового. Мы сформулируем его ради полноты.

4.34. Теорема. Пусть f и g определены на Е. Допустим, что

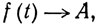
g(t)→B при t→x.

Тогда

(а) если f(t)→A', то А' = А,

(b) (f+g)(t)→A+B,

(с) (fg)(t)→AB,

(d) (f/g)(t)→A/B,

если правые части в (b), (с) и (d) имеют смысл.

Напомним, что ∞ -∞ , 0*∞, ∞/∞, А/0 не определялись (см. определение 1.39).