Упражнения

1. Доказать, что функция f, заданная равенством

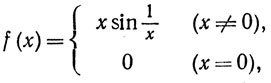
непрерывна при х = 0. Нарисовать график этой функции.

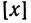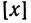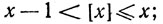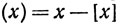2. Пусть обозначает наибольшее из целых чисел, не превосходящих числа х, т. е. - такое целое число, что пусть (обозначает дробную часть числа х. Какие разрывы имеют функции 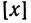и (x)?

3. Пусть f - вещественная равномерно непрерывная функция на ограниченном множестве Е в R¹. Доказать, что f ограничена на Е.

4. Пусть f - вещественная функция, заданная на (а, b). Доказать, что множество точек, в которых f имеет простой разрыв, не более чем счетно.

Указание. Пусть Е - множество, на котором 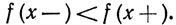Каждой точке х множества Е сопоставим тройку (р, q, r) рациональных чисел, таких, что

(a) f(x-)<р<f(x+),

(b) при a<q<t<t&360;x имеем f(t)<р,

(c) при x<t<r&360;b имеем f(t)>p.

Множество всех таких троек не более чем счетно. Показать, что каждой такой тройке отвечает не более одной точки множества Е. Подобным образом следует действовать и в случае других типов простого разрыва.

5. Каждое рациональное число х можно записать в виде х = ^m/_n, где n>0, m и n - взаимно простые целые числа. Если х = 0, то мы полагаем n = 1. Рассмотрим функцию f, заданную на R¹ равенством

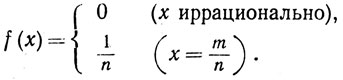
Доказать, что f непрерывна в каждой иррациональной точке и имеет простой разрыв в каждой рациональной точке.

6. Пусть f - вещественная непрерывная функция, заданная на замкнутом множестве Е⊂R¹. Доказать, что существует непрерывная вещественная функция g на R¹, такая, что f(х) - g(x) при всех х∈Е (такая функция называется непрерывным продолжением функции f с множества Е на R¹). Показать, что результат перестает быть верным, если опустить предположение замкнутости. Распространить результат на векторнозначные функции.

Указание. График функции g - прямолинейный отрезок над каждым из интервалов, составляющих дополнение множества Е (ср. с упражнением 15, гл. 2). Результат остается верным, если R¹ заменить любым метрическим пространством, но доказательство уже не так просто.

7. Если функция f определена на Е, то графиком f называется множество пар (х, f(х)), где х∈Е. В частности, если E - множество вещественных чисел, а функция f вещественна, то графиком f служит некоторое подмножество плоскости.

Допустим, что Е компактно. Доказать, что f непрерывна на Е в том и только в том случае, когда ее график компактен.

8. Если Е⊂X, а f - функция, заданная на X, то сужением f на Е называется функция g, определенная на множестве Е и такая, что g(p) = f(р) при р∈Е. Зададим в R² функции f и g равенствами: f(0, 0) = g(0, 0)-0,

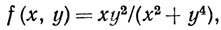
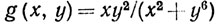
при (х, у)≠(0, 0). Доказать, что f ограничена на R², что g не ограничена в любой окрестности точки (0, 0) и что f разрывна в точке (0, 0); тем не менее сужения каждой из функций f и g на любую прямую в R непрерывны!

9. Пусть f - непрерывное отображение метрического пространства X в метрическое пространство Y. Пусть Е - замкнутое подмножество пространства Y. Доказать, что множество f^-1(E) замкнуто в X.

10. Пусть f - непрерывная вещественная функция на метрическом пространстве X. Пусть Z(f) (нуль-множество функции f) есть множество всех р∈Х, в которых f(р) = 0. Доказать, что множество Z(f) замкнуто.

11. Если Е - непустое подмножество метрического пространства X, то определим расстояние от точки х∈X до множества Е равенством

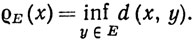
(a) Доказать, что 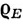(x) = 0 тогда и только тогда, когда х принадлежит замыканию множества Е.

(b) Доказать, что 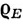- равномерно непрерывная функция на X.

Указание. Мы имеем 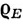(x₂)≤d(х₂, у)≤d(х₂, x₁) + d(x₁, у), так что

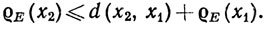
12. Пусть К и F - непересекающиеся подмножества метрического пространства X, причем К компактно, F замкнуто. Доказать, что существует число δ>0, такое, что d(p, q)>δ, если р∈K, q∈F.

Указание. Функция 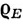- положительная непрерывная функция на К.

Показать, что это утверждение может оказаться неверным, если ни одно из двух непересекающихся замкнутых множеств не компактно.

13. Пусть А и В - непустые непересекающиеся замкнутые множества в метрическом пространстве X. Положим

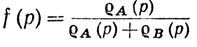
Показать, что f - непрерывная функция на X, множество значений которой содержится в сегменте [0, 1]; что f(р) = 0 в точках множества А и только в них; что f(р) = 1 в точках множества В и только в них. Тем самым установлено утверждение, обратное к теореме упражнения 10: каждое замкнутое множество A⊂X является нуль-множеством для некоторой вещественной непрерывной функции f на X. Полагая

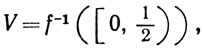
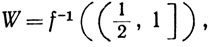
показать, что V и W открыты, не пересекаются и AͳV, B⊂W. (Таким образом, каждое из двух непересекающихся замкнутых множеств в метрическом пространстве может быть накрыто открытым множеством так, что и эти открытые множества не пересекаются. Это свойство метрических пространств называют нормальностью.)

14. Назовем отображение пространства X в пространство Y открытым, если f(V) открыто в Y, каково бы ни было открытое множество V в X.

Доказать, что каждое непрерывное открытое отображение R¹ в R¹ монотонно.

15. Пусть f и g - непрерывные отображения метрического пространства X в метрическое пространство Y, и пусть Е - всюду плотное подмножество из X. Доказать, что f(E) плотно в f(X). Доказать, что если f(p) = g(p) при всех р∈Е, то f(p) = g(p) при всех рбХ. (Иными словами, непрерывное отображение определяется своими значениями на всюду плотном подмножестве своей области определения.)

16. Показать, что определение равномерной непрерывности можно следующим образом сформулировать, используя понятие диаметра множества: для каждого ε>0 существует δ>0, такое, что diam f(Е)<ε для любого Е⊂X, для которого diam Е<δ.

17. Пусть Е - плотное подмножество метрического пространства X, и пусть f - равномерно непрерывная вещественная функция, заданная на Е. Доказать, что f имеет непрерывное продолжение с E на X (по поводу терминологии см. упражнение 6). (Единственность следует из упражнения 15.)

Указание. Для каждой точки р∈X и каждого положительного целого n пусть V_n(p) - множество всех q∈E, таких, что d(p, q)<¹/_n. Воспользоваться упражнением 16 для доказательства того, что пересечение замыканий множеств f(V₁(p)), f(V₂(p)), ... состоит из единственной точки пространства R1, которую мы обозначим через g (p). Доказать, что функция g, определенная таким образом на X, и есть требуемое продолжение функции f.

Можно ли пространство значений R¹ заменить здесь пространством R^k? Любым компактным метрическим пространством? Любым полным метрическим пространством? Любым метрическим пространством?

18. Вещественная функция f, заданная на (а, b), называется выпуклой, если

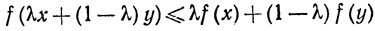
при любых a<x<b, a<y<b, 0<λ<1. Доказать, что каждая выпуклая функция непрерывна. Доказать, что каждая возрастающая выпуклая функция от выпуклой функции выпукла (например, если f выпукла, то e^f тоже выпукла).

19. Провести подробно следующий вариант доказательства теоремы 4.19: если f не равномерно непрерывна, то для некоторого ε>0 существуют две последовательности {р_n}, {q_n} в X, такие, что d_X(p_n, q_n)→0, но d_Y(f(p_n), f(q_n))>ε. Воспользоваться теоремой 2.37, чтобы получить противоречие.