(25)

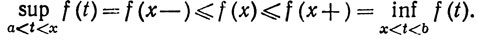
Кроме того, если a<x<y<b, то

(26)

Аналогичные результаты, очевидно, верны и для монотонно убывающих функций.

Доказательство. По предположению, множество чисел f(t), где a<t<x, ограничено сверху числом f(x) и потому имеет верхнюю грань, которую мы обозначим через А. Очевидно, что A≤f(x). Мы должны показать, что A = f(x-).

Пусть задано ε>0. Из определения числа А следует, что существует число δ>0, такое, что а<x-δ<x и

(27)

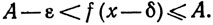
Поскольку f монотонна, имеем

(28)

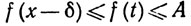
Комбинируя неравенства (27) и (28), мы получаем

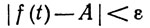
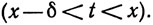
Значит, f(x-) = A.

Вторая часть неравенства (25) доказывается точно таким же способом.

Далее, если а<х<у<b, то из (25) следует, что

(29)

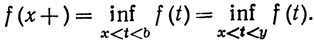
Последнее равенство получится, если применить (25) к (а, у) вместо (а, b).

Подобным же образом

(30)

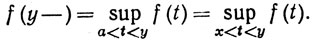
Сравнение равенств (29) и (30) дает неравенство (26).

Следствие.Монотонная функция не имеет разрывов второго рода.

Из этого следствия вытекает, что монотонная функция может иметь разрывы только в конечном или счетном множестве точек. Вместо того чтобы сослаться на общую теорему, доказательство которой намечено в упражнении 4, мы дадим здесь простое доказательство, применимое к монотонным функциям.

4.30. Теорема. Пусть функция f монотонна на интервале (а, b). Тогда множество точек интервала (а, b), в которых f разрывна, не более чем счетно.

Доказательство. Допустим для определенности, что f возрастает, и пусть Е - множество точек, в которых f разрывна.

Каждой точке х∈Е сопоставим рациональное число r(x), такое, что

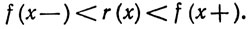
Ясно, что r(х₁)≠r(х₂), если х₁≠х₂, так как при x₁<x₂ мы имеем f(x₁+)≤f(x₂-).

Таким образом установлено взаино однозначное соответствие между множеством E и подмножеством множества всех рациональных чисел. Это последнее множество, как мы знаем, счетно.

4.31. Замечание. Нужно отметить, что точки разрыва монотонной функции не обязаны быть изолированными. В самом деле, для любого счетного подмножества E интервала (a, b), которое может быть даже всюду плотным, можно построить функцию f, монотонную на (a,b), имеющую разрыв в каждой точке множества Е и непрерывную во всех остальных точках интервала (a,b).

Чтобы доказать это, расположим точки множества Е в последовательность {x_n}, n = 1, 2, 3, ... . Пусть {c_n} - последовательность положительных чисел, такая, что ряд ∑ c_n сходится. Положим

(31)

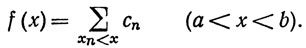
Для вычисления этой суммы нужно сложить все с_n, индексы которых таковы, что x_n<x. Если слева от х нет точек x_n, то сумма пуста и, следуя обычному соглашению, мы считаем ее равной нулю. Поскольку ряд (31) сходится абсолютно, порядок, в котором выписываются его члены, не существен.

Мы предоставляем читателю проверку следующих свойств функции f:

(a) f монотонно возрастает на (а, b);

(b) f разрывна в каждой точке множества Е; действительно,

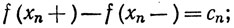
(c) f непрерывна во всех остальных точках интервала (а, b). Более того, нетрудно видеть, что f(х -) = f(x) во всех точках

интервала (а, b). Если функция f удовлетворяет этому условию, то мы будем говорить, что она непрерывна слева. Если бы в (31) суммирование производилось по всем индексам л, для которых х_n≤х, то мы имели бы f(х+) = f(x) во всех точках интервала (а, b), т. е. f была бы непрерывной справа.

Функции такого типа можно строить и другим методом; пример читатель найдет в упражнении 5 гл. 6.