Разрывы функций

Если х - точка из области определения функции f, в которой эта функция не является непрерывной, то мы будем говорить, что f разрывна в х или что f имеет разрыв в х. Если функция f определена на интервале или на сегменте, то удобно выделить разрывы двух типов. Прежде чем произвести эту классификацию, мы должны определить правосторонний и левосторонний пределы функции f в точке х, которые мы обозначим соответственно через f(x+) и f(x-).

4.25. Определение. Пусть функция f определена на интервале (а, b). Рассмотрим любую точку х, такую, что а≤x<b. Мы будем писать

если f(t_n)→q при n→∞ для всех последовательностей {t_n}, содержащихся в интервале (х, b), таких, что t_n→x. Чтобы получить определение предела f(x-) (в случае а<x≤b), мы ограничимся последовательностями {t_n}, содержащимися в (а, х).

Ясно, что в любой точке интервала (а, b) предел 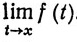существует тогда и только тогда, когда

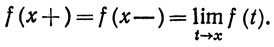
4.26. Определение. Пусть функция f определена на интервале (а, b). Если f разрывна в точке х и если f(x+) и f(x-) существуют, то говорят, что f имеет в точке х разрыв первого рода, или простой разрыв. В противном случае разрыв называется разрывом второго рода.

Возможны две разновидности простых разрывов: либо 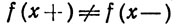(в этом случае значение f(x) несущественно), либо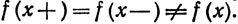

4.27. Примеры, (а) Положим

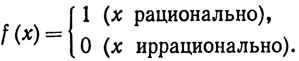
Тогда f имеет разрывы второго рода во всех точках х, так как ни f(x+), ни f(x-) не существуют.

(b) Положим

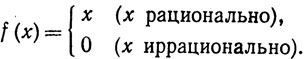
Тогда f непрерывна в точке x = 0 и имеет разрывы второго рода во всех остальных точках.

(c) Положим

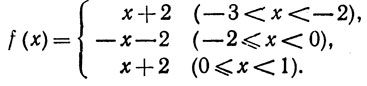
Тогда f имеет простой разрыв в точке x = 0 и непрерывна во всех остальных точках интервала (-3, 1).

(d) Положим

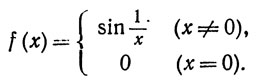
Поскольку ни f(0+), ни f(0-) не существуют, функция f имеет разрыв второго рода в точке x = 0. Мы еще не доказали, что sinx - непрерывная функция. Если считать это утверждение верным, то из теоремы 4.7 следует, что f непрерывна в каждой точке х≠0.