Непрерывность и компактность

4.13. Определение. Отображение f множества Е в пространство R^л называется ограниченным, если существует вещественное число М, такое, что 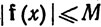для всех х∈Е.

4.14. Теорема. Пусть f - непрерывное отображение компактного метрического пространства X в метрическое пространство Y. Тогда множество f (X) компактно.

Доказательство. Пусть {V_α} - открытое покрытие множества f(X). Поскольку f непрерывно, теорема 4.8 показывает, что все множества f^-1(V_α) открыты. Так как X компактно, имеется конечный набор индексов а₁, ...,а_n, такой, что

(12)

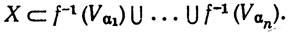
Поскольку f(f^-1(E)) = E при каждом E⊂Y, из (12) следует, что

(13)

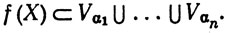
Доказательство закончено.

Замечание. Мы воспользовались соотношением f(f^-1(E)) = E, которое верно при Е⊂Y. Если Е⊂X, то можно утверждать лишь, что f^-1(f(E)) = E; равенства может и не быть.

Выведем теперь некоторые следствия из теоремы 4.14.

4.15. Теорема. Если f - непрерывное отображение компактного метрического пространства X в пространство R^k, то множество f(X) замкнуто и ограничено. Таким образом, отображение f ограничено.

Это следует из теоремы 2.41. Этот результат особенно важен тогда, когда f - вещественная функция.

4.16. Теорема. Пусть f - непрерывная вещественная функция на компактном метрическом пространстве X и

(14)

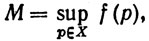
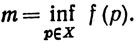
Тогда существуют точки p,q∈X, такие, что f(p) = M и f(q) = m.

Обозначения в (14) имеют следующий смысл: М - верхняя грань множества всех чисел f (р), когда р пробегает X, а m - нижняя грань этого числового множества.

Утверждение теоремы можно сформулировать и так: существуют точки р и q в X, такие, что f(q)≤f(х)≤f(р) для всех x∈Х, т. е. функция f достигает своего максимума (в точке р) и минимума (в точке а).

Доказательство. По теореме 4.15 f(X) - ограниченное и замкнутое множество вещественных чисел; значит, f(X) содержит свою верхнюю и нижнюю грани (теорема 2.28).

4.17. Теорема. Пусть f - непрерывное взаимно однозначное отображение компактного метрического пространства X на метрическое пространство Y. Тогда обратное отображение f^-1, определенное на Y равенством

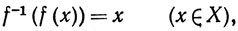
есть непрерывное отображение множества Y на X.

Доказательство. Применяя теорему 4.8 к f^-1 вместо f, мы видим, что достаточно доказать, что f(V) - открытое множество в Y для каждого открытого в X множества V. Зафиксируем такое множество V.

Дополнение V^c множества V замкнуто в X и, следовательно, компактно (теорема 2.35); значит, f(V^c) - компактное подмножество множества Y (теорема 4.14); поэтому оно замкнуто в Y (теорема 2.34). Поскольку f взаимно однозначно отображает X на Y, множество f(V) совпадает с дополнением множества f(V^c). Значит, f(V) открыто.

4.18. Определение. Пусть f - отображение метрического пространства X в метрическое пространство Y. Мы будем говорить, что отображение f равномерно непрерывно на X, если для каждого ε>0 существует δ>0, такое, что

(15)

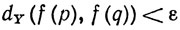
для всех р и q из X, для которых d_X (p, q)<δ.

Посмотрим, чем отличаются понятия непрерывности и равномерной непрерывности. Во-первых, равномерная непрерывность есть свойство функции на множестве, тогда как непрерывность может быть определена в одной точке. Бессмысленно спрашивать, является ли данная функция равномерно непрерывной в некоторой точке. Во-вторых, если f непрерывна на X, то для каждого ε>0 и для каждой точки р множества X можно найти число δ>0, обладающее свойством, указанным в определении 4.5. Это δ зависит от ε и от р. Если же f равномерно непрерывна на X, то для каждого ε>0 можно найти одно число δ>0, которое годится для всех точек р множества X.

Очевидно, каждая равномерно непрерывная функция непрерывна. В случае компактных множеств эти два понятия, как показывает следующая теорема, равносильны.

4.19. Теорема. Пусть f - непрерывное отображение компактного метрического пространства X в метрическое пространство Y. Тогда f равномерно непрерывно на X.

Доказательство. Пусть ε>0. Поскольку f непрерывно, каждой точке р∈Х можно сопоставить положительное число φ(р), такое, что

(16) если q∈X, d_X (p,q)<φ(p), то d_Y (f(p), f(q))<^ε/₂.

Пусть J(p) - множество всех q∈X, для которых

(17)

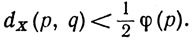
Поскольку p∈J(p), семейство всех множеств J(p) образует открытое покрытие пространства X, а поскольку пространство X компактно, в нем найдется конечное множество точек р₁, ..., p_n, такое, что

(18)

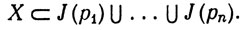
Положим

(19)

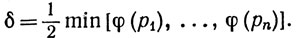
Тогда δ>0. (Именно здесь существенна конечность покрытия, упоминаемого в определении компактности. Минимум конечного числа положительных чисел положителен, тогда как нижняя грань бесконечного множества положительных чисел вполне может оказаться равной нулю.)

Пусть теперь q и р - точки множества X, такие, что d_X (p, q)<δ. Согласно (18), существует целоет, 1≤n≤n, такое, что p∈J(p_m). Значит,

(20)

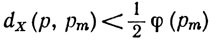
и, кроме того,

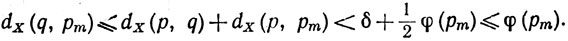
Наконец, из (16) следует, что тогда

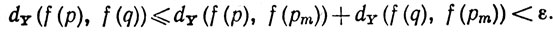
Доказательство закончено.

Другое доказательство намечено в упражнении 19. Теперь мы перейдем к доказательству того, что компактность существенна в предположениях теорем 4.14, 4.15, 4.16 и 4.19.

4.20. Теорема. Пусть Е - некомпактное множество в R¹.

(с) Если, кроме того, множество Е ограничено, то существует непрерывная на Е функция, не являющаяся равномерно непрерывной.

Доказательство. Допустим сначала, что Е ограничено, так что существует предельная точка х0 множества Е, не содержащаяся в Е.

Рассмотрим функцию

(21)

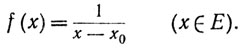
Эта функция непрерывна на Е (теорема 4.9), но, очевидно, не ограничена. Убедимся в том, что функция (21) не является равномерно непрерывной. Пусть ε>0 и δ>0 произвольны. Выберем точку х∈Е, такую, что |х-х₀|<δ. Взяв t достаточно близким к х₀, мы можем сделать разность |f(t)-f(x)| больше ε, хотя |t-х|<δ. Поскольку это верно при любом δ>0, функция f не является равномерно непрерывной на Е.

Функция g, заданная равенством

(22)

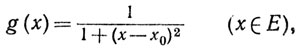
непрерывна на E и ограничена, так как 0<g(x)<1. Ясно, что

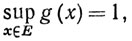
тогда как g(х)<1 при всех х∈Е. Таким образом, g не имеет максимума на Е.

Доказав теорему для ограниченных множеств Е, предположим, что Е не ограничено. Тогда свойство (а) выполняется для функции f(x) = x, а свойство (b) - для функции

(23)

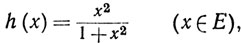
так как

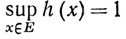
и h(х)<1 при всех х∈Е.

Утверждение (с) неверно, если не предполагать, что множество Е ограничено. Действительно, пусть Е - множество всех целых чисел. Тогда любая функция, заданная на Е, равномерно непрерывна на Е. Чтобы убедиться в этом, нужно всего лишь взять δ<1 в определении 4.18.

В заключение этого раздела мы покажем, что компактность существенна также и в теореме 4.17.

4.21. Пример. Пусть X - полуинтервал [0, 2π) вещественной оси и пусть f - отображение множества X на окружность Y, состоящую из всех точек, удаленных от начала на расстояние 1, заданное равенством

(24)

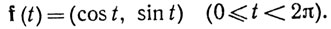
Непрерывность тригонометрических функций (косинуса и синуса), так же как и их периодичность, будут установлены в главе 8. Принимая эти факты без доказательства, легко видеть, что f - непрерывное взаимно однозначное отображение множества X на Y.

Однако обратное отображение (которое существует, так как f взаимно однозначно отображает X на Y) не непрерывно в точке (1,0) = f(0). Конечно, в этом примере X некомпактно. (Любопытно, что f^-1 не непрерывно, несмотря на то, что Y компактно!)