Непрерывные функции

4.5. Определение. Пусть X и Y - метрические пространства, E⊂X, р∈Е и f отображает Е в Y. Тогда функция f называется непрерывной в точке р, если для любого ε>0 существует δ>0, такое, что

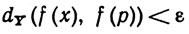
для всех точек х∈Е, для которых d_X (x, р)<δ.

Если f непрерывна в каждой точке множества Е, то f называется непрерывной на Е.

Для того чтобы быть непрерывным в точке р, отображение должно быть определено в этой точке. (Ср. это с замечанием, следующим за определением 4.1.)

Если р - изолированная точка множества Е, то из нашего определения следует, что каждая функция /, определенная на Е, непрерывна в точке р. Действительно, каково бы ни было ε>0, можно указать δ>0, такое, что единственной точкой х∈Е, для которой d_X (x, р)<δ, окажется x = р; тогда

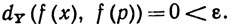
4.6. Теорема.В ситуации, описанной в определении 4.5, предположим, что р - предельная точка множества Е. Функция f непрерывна в точке р тогда и только тогда, когда 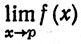= f(p).

Доказательство. Это становится ясным, если сравнить определения 4.1 и 4.5.

Теперь перейдем к сложным функциям. Краткая формулировка следующей теоремы такова: непрерывная функция от непрерывной функции непрерывна.

4.7. Теорема.Пусть X, Y, Z - метрические пространства, E⊂X, f отображает множество Е в Y, g отображает множество значений f, а именно f(E), в Z и h - отображение множества Е в Z, определенное равенством

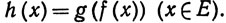
Если f непрерывно в точке р∈Е, a g непрерывно в точке f(р), то h непрерывно в точке р.

Доказательство. Пусть ε>0. Поскольку g непрерывно в точке f(p), существует η>00, такое, что

Поскольку f непрерывно в точке р, существует δ>0, такое, что

Следовательно,

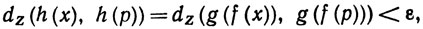
если d_X (x, р)< и х∈Е. Таким образом, h непрерывно в точке р.

4.8. Теорема. Отображение f метрического пространства X в метрическое пространство Y непрерывно на X тогда и только тогда, когда множество f^-1 (V) открыто в X для каждого открытого множества V из Y.

(Прообразы были определены в п. 2.4.) Это очень полезное свойство, характеризующее непрерывность.

Доказательство. Допустим, что f непрерывно на X; пусть V - открытое множество в Y. Мы должны показать, что каждая точка множества f^-1(K) является его внутренней точкой. Итак, пусть р∈Х и f(p)∈V. Поскольку V открыто, существует ε>0, такое, что y∈V, если d_Y (f(p), y)<ε, а так как f непрерывно в точке р, то существует δ>0, такое, что d_Y (f(x), f(p))<ε, если d_X (x, р)<δ. Таким образом, x∈f^-1(V), как только d_X (x, p)<δ.

Обратно, допустим, что множество f^-1(V) открыто в X, каково бы ни было открытое множество V в Y. Зафиксируем р∈Х и ε>0, и пусть V - множество всех y∈Y, таких, что d_Y (y, f(p))<ε. Тогда V открыто, а поэтому и f^-1 (V) открыто; значит, существует δ>0, такое, что x∈f^-1(V), как только d_X (p, x)<δ. Но если x∈f^-1(V), то f(x)∈V, так что d_Y (f(x), f(p))<ε.

Доказательство закончено.

Обратимся теперь к комплекснозиачным и векторнозначным функциям и к функциям, определенным на подмножествах пространства R^k.

4.9. Теорема. Пусть f и g - комплексные непрерывные функции на метрическом пространстве X. Тогда f+g, fg и f/g непрерывны на X.

В последнем случае мы должны, конечно, предполагать, что g(x)≠0 при всех х∈Х.

Доказательство. В случае изолированной точки доказывать нечего. В случае предельней точки утверждение следует из теорем 4.4 и 4.6.

4.10. Теорема, (а) Пусть f₁, ..., f_k - вещественные функции на метрическом пространстве X, и пусть f - отображение пространства X в R^k, определенное равенством

(7)

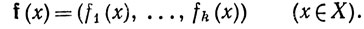
Отображение f непрерывно тогда и только тогда, когда каждая из функций f₁, ..., f_k непрерывна.

(b) Если f и g - непрерывные отображения пространства X в R^k, то f+g и f-g непрерывны на X.

Функции f₁, ..., f_k называются компонентами отображения f. Отметим, что f+g - отображение в R^k, тогда как f-g - вещественная функция на X.

Доказательство. Утверждение части (а) следует из неравенств

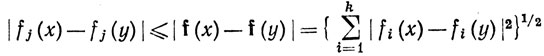
при j = 1, ..., k. Часть (b) следует из (а) и теоремы 4.9.

4.11. Примеры. Если x₁, ..., x_k - координаты точки x∈R^k, то функции φ_i, определенные равенствами

(8)

непрерывны на R^k, так как неравенство

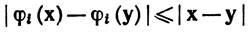
показывает, что в определении 4.3 можно положить δ = ε. Функции φ_i иногда называются координатными функциями. Повторное применение теоремы 4.9 показывает, что каждый одночлен

(9)

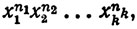
где n₁,. ..., n_k - неотрицательные целые числа, непрерывен в R_k. То же верно в отношении функций, отличающихся от (9) постоянным множителем, так как постоянные, очевидно, непрерывны. Следовательно, каждый многочлен Р, заданный равенством

(10)

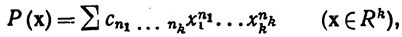
непрерывен на R^k. Здесь коэффициенты с_n1, ... _nk - комплексные числа, n₁, ..., n_k - неотрицательные целые числа, а сумма содержит конечное число слагаемых.

Далее, всякая рациональная функция от х₁, ... , x_k, т. е. каждое отношение двух многочленов вида (10), непрерывна на R^k всюду, где знаменатель отличен от нуля.

Из неравенства треугольника легко получаем, что

(11)

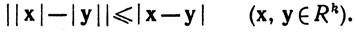
Значит, отображение, ставящее в соответствие каждому х величину |х|, является непрерывной вещественной функцией на R^k.

Если f - непрерывное отображение метрического пространства X в пространство R^k и если φ определено на X равенством φ(р) = |f(p)|, то из теоремы 4.7 следует, что φ - непрерывная вещественная функция на X.

4.12. Замечание. Мы определили понятие непрерывности для функций, заданных на подмножестве Е метрического пространства X. Однако дополнение множества Е в X не играет никакой роли в этом определении, в отличие от определения пределов функций. Тем самым мы можем говорить о непрерывных отображениях одного метрического пространства в другое (а не об отображениях подмножеств). Это упрощает формулировки и доказательства некоторых теорем. Мы уже воспользовались этим в теоремах 4.8 - 4.10 и будем поступать так же в разделах, посвященных компактности и связности.