Предел функции

4.1. Определение. Пусть X и Y - метрические пространства. Пусть Е⊂Х, f отображает Е в У, а р - предельная точка множества Е. Мы будем писать "f(x)→q при х→р", или

(1)

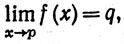
если существует точка q∈Y, обладающая следующим свойством: для любого ε>0 существует δ>0, такое, что

(2)

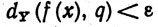
для любых точек х∈Е, для которых

(3)

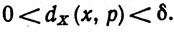
Символы d_X и d_Y относятся к расстояниям соответственно в пространствах X и Y.

Если X и (или) Y заменяются вещественной прямой, комплексной плоскостью или каким-нибудь евклидовым пространством R^k, то расстояния d_X, d_Y, конечно, заменяются абсолютными величинами или соответствующими нормами (см. п. 2.18).

Следует отметить, что р∈Х, но точка р не обязана принадлежать множеству Е в предыдущем определении. Более того, даже если р∈Е, то вполне возможно, что f(p ≠.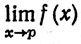

Этому определению можно придать другую форму, высказав его в терминах последовательностей.

4.2. Теорема. Пусть X, Y, Е, f и р - те же, что и в определении 4.1. Тогда

(4)

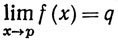
в том и только в том случае, когда

(5)

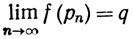
для любой последовательности {р_n}, такой, что

(6)

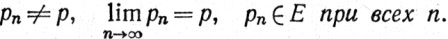
Доказательство. Допустим, что выполнено равенство (4). Выберем какую-нибудь последовательность {р_n}, удовлетворяющую условию (6). Пусть ε>0. Тогда существует δ>0, такое, что d_Y{f{x), q)<ε, если х∈Е и 0<d_X(p, х)<δ. Кроме того, существует N, такое, что при n>N имеем 0<d_X(р_n, р)<δ. Таким образом, при n>N имеем d_Y(f(р_n), q)<ε, откуда следует, что выполнено равенство (5).

Обратно, допустим, что (4) неверно. Тогда существует число ε>0, такое, что для каждого δ>0 найдется точка х∈Е (зависящая от δ), для которой d_Y(f(x),q)≥ε, но 0<d_X(х, р)<δ. Выбирая δ_n = ¹/_n (n = 1, 2, 3, ...), мы найдем последовательность, удовлетворяющую условию (6), для которой равенство (5) не выполняется.

Следствие.Если f имеет предел в точке р, то этот предел единственный.

Это следует из теорем 3.2 (6) и 4.2.

4.3. Определение. Пусть на Е определены две комплексные функции f и g. Символом f+g обозначается функция, сопоставляющая каждой точке х множества Е число f(x)+g(x). Подобным образом мы определим разность f-g, произведение fg и отношение f/g двух функций, имея в виду, что отношение определено лишь в тех точках х∈Е, в которых g(x)≠0. Если f сопоставляет каждой точке х множества Е одно и то же число с, то f называется постоянной функцией, или просто постоянной, и мы будем писать в этом случае f = c. Если f и g - вещественные функции и если f(x)≥g(x) при каждом х∈Е, то мы иногда для краткости будем писать f≥g.

Аналогично, если f и g отображают Е в R^k, то мы определим f+g и f*g равенствами (f+g)(x) = f(x)+g(x), (f*g)(x) = f(x)*g(x), и если λ - вещественное число, то (λf)(х) = λf(х).

4.4. Теорема. Пусть X - метрическое пространство, Е⊂Х, р - предельная точка множества Е, f и g - комплексные функции на Е и

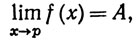
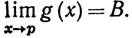
Тогда

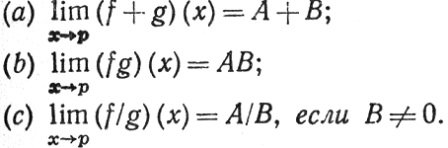
Доказательство. Эти утверждения, в силу теоремы 4.3, немедленно следуют из аналогичных свойств последовательностей (теорема 3.3).

Замечание. Если f и g отображают Е в R^k, то (а) остается верным, а (b) принимает вид

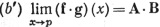
(ср. с теоремой 3.4).