Упражнения

1. Доказать, что из сходимости последовательности {s_n} следует сходимость последовательности {|s_n|}. Верно ли обратное?

2. Вычислить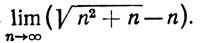

3. Пусть 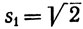и

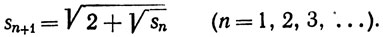
Доказать, что последовательность {s_n} сходится и что s_n<2 при n = 1, 2, 3, ... .

4. Найти верхний и нижний пределы последовательности {s_n}, определенной следующим образом:

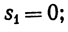
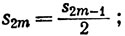
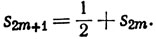
5. Для любых двух вещественных последовательностей {а_n}, {b_n} имеем

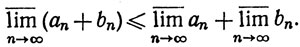
6. Исследовать поведение (сходимость или расходимость ряда) ∑a_n если

(a)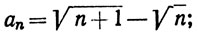

(b)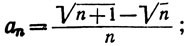

(c)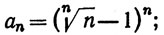

(d) 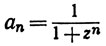для комплексных значений z.

7. Доказать, что из сходимости ряда ∑a_n следует сходимость ряда

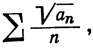
если а_n≥0.

8. Если ряд ∑a_n сходится и если {b_n} - монотонная и ограниченная последовательность, то и ряд ∑a_nb_n сходится.

9. Найти радиус сходимости каждого из следующих степенных рядов:

(a)

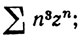
(b)

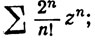
(c)

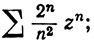
(d)

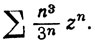
10. Допустим, что коэффициенты степенного ряда ∑a_nzⁿ - целые числа, среди которых бесконечно много отличных от нуля.

Доказать, что радиус сходимости не превышает единицы.

11. Допустим, что ряд ∑a_n расходится, а_n>0, и пусть s_n = a₁ + ... + а_n. Доказать, что

(a) ряд 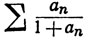расходится;

(b) ряд 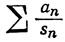расходится;

(c) ряд 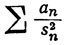сходится.

Что можно сказать о рядах ,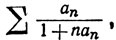

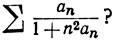
12. Допустим, что ряд 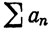сходится, а_n>0, и положим

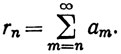
Доказать, что

(а) ряд 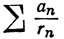расходится;

(б) ряд 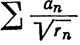сходится.

13. Доказать, что произведение Коши двух абсолютно сходящихся рядов сходится абсолютно.

14. Пусть {s_n} - какая-нибудь последовательность. Рассмотрим средние арифметические

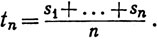
Доказать, что из сходимости s_n→s следует сходимость t_n→s. Доказать, что существуют расходящиеся последовательности {s_n}, которым соответствуют сходящиеся последовательности {t_n}.

15. Определение 3.21 можно распространить на тот случай, когда ап принадлежат некоторому фиксированному пространству R^k. Абсолютная сходимость определяется как сходимость ряда ∑|a_n|. Показать, что теоремы 3.22, 3.23, 3.25, 3.33, 3.34, 3.42, 3.45, 3.47, 3.56 и 3.57 остаются верными в этом более общем случае (доказательства требуют лишь незначительных изменений).

16. Доказать следующий аналог теоремы 3.10 (b): если {Е_n} - убывающая последовательность замкнутых множеств в полном метрическом пространстве X и если

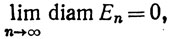
то множество 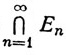состоит ровно из одной точки.

17. Пусть X - полное метрическое пространство, a {G_n} - последовательность всюду плотных открытых подмножеств пространства X. Доказать теорему Бэра, состоящую в том, что множество 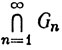непусто. (В действительности оно плотно в X.)

Указание. Найти стягивающуюся последовательность замкнутых окрестностей Е_n, таких, что Е_n⊂G_n, и применить упражнение 16.

18. Пусть {р_n} и {q_n} - последовательность Коши в метрическом пространстве X. Показать, что последовательность {d(p_n, q_n)} сходится.

Указание. Для любых m, n имеем d(p_n, q_n)≤d(p_n, р_m) + d(p_m, q_m) + d(q_m, q_n), следовательно, разность

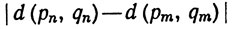
мала, если m, n велики.

19. Пусть X - метрическое пространство. (а) Назовем две последовательности Коши {р_n}, {q_n} в X эквивалентными, если

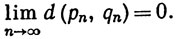
Доказать, что этим определено отношение эквивалентности^*.

^* (Это означает, что 1) всякая последовательность Коши эквивалентна самой себе; 2) из эквивалентности пары последовательностей {p_n}, {q_n} следует эквивалентность пары {q_n}, {p_n}; 3) из эквивалентности пар {р_n}, {q_n} и {q_n}, {r_n} следует эквивалентность пары последовательностей {р_n}, {r_n}.- Прим. перев.)

(b) Пусть X^* - множество всех полученных таким образом классов эквивалентности^*. Если Р∈Х*, Q∈Х*, {р_n}∈Р, {qn}∈Q, то положим, по определению,

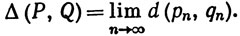
^* (Классом эквивалентности называется множество всех последовательностей Коши, эквивалентных какой-нибудь одной последовательности.- Прим. перев.)

В силу упражнения 18, этот предел существует. Показать, что число Δ(Р, Q) не изменится, если {р_n} и {q_n} заменить эквивалентными последовательностями, и что тем самым Δ - расстояние на X^*.

(с) Доказать, что полученное метрическое пространство X^* полно.

(d) Каждому р∈Х сопоставим последовательность Коши, все члены которой равны р; пусть Р_р - тот элемент множества X^*, который содержит эту последовательность. Доказать, что

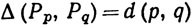
при всех р, q∈X. Иными словами, отображение φ, заданное равенством φ(р) = Р_р, есть изометрия (т. е. отображение, сохраняющее расстояния) пространства X в X^*.

(е) Доказать, что φ(Х) всюду плотно в X^* и что φ(Х) = Х^*, если X полно.

В силу (d) можно отождествить X с φ(Х) и, таким образом, считать, что X погружено в полное метрическое пространство X^*. Мы будем называть X^*пополнением пространства X.

20. Пусть X - пространство рациональных чисел с метрикой 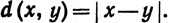Что служит пополнением этого пространства? (Ср. с упражнением 19.)