Перестановки рядов

3.52. Определение. Пусть {k_n}, n = 1, 2, 3, ..., - последовательность, в которой каждое положительное целое число встречается один и только один раз (т. е. {К} - взаимно однозначное отображение множества J на J, см. определение 2.4). Положим

мы будем говорить, что ряд ∑a'_n является перестановкой ряда ∑a_n.

Если {s_n}, {s'_n} - последовательности частных сумм рядов ∑a_n, ∑a'_n, то легко видеть, что, вообще говоря, эти две последовательности составлены из совершенно разных чисел. Мы, таким образом, приходим к задаче: выяснить, при каких условиях все перестановки сходящегося ряда сходятся и совпадают ли их суммы между собой.

3.53. Определение. Говорят, что ряд ∑a_n сходится безусловно, если каждая его перестановка сходится (к той же сумме). (Ср. с теоремой 3.57.)

3.54. Пример. Рассмотрим сходящийся ряд

(22)

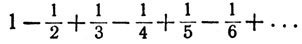
и одну из его перестановок

(23)

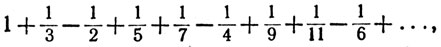
в которой за двумя положительными членами всегда следует отрицательный. Если s - сумма ряда (22), то

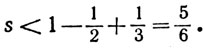
Так как

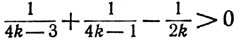
при k≥1, то мы видим, что s'₃<s₆'<s₉'< ..., где s'_n есть n-я частная сумма ряда (23). Значит,

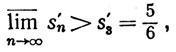
так что ряд (23) наверняка не сходится к s [мы предоставляем читателю проверку того, что ряд (23) тем не менее сходится].

Этот пример иллюстрирует следующую теорему, принадлежащую Риману.

3.55. Теорема. Пусть ∑a_n - неабсолютно сходящийся ряд вещественных чисел, и пусть α≤β - два данных числа (в расширенной системе вещественных чисел). Тогда существует перестановка ∑a'_nc с частными суммами s'_n, такая, что

(24)

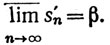
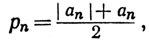
Доказательство. Пусть

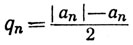
Тогда р_n - q_n = а_n, 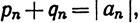p_n≥0, q_n≥0. Ряды ∑p_n, ∑q_n оба должны расходиться.

Действительно, если бы оба эти ряда сходились, то и ряд

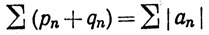
сходился бы, вопреки предположению. Сходимость ряда ∑q_n и расходимость ряда ∑p_n (или наоборот) влечет за собой расходимость ряда ∑a_n, что снова противоречит предположению, так как

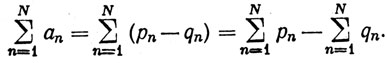
Обозначим теперь через Р₁, Р₂, Р₃, ... неотрицательные члены ряда ∑a_n в том порядке, в каком они встречаются, и пусть Q₁, Q₂, Q₃, ... - абсолютные величины отрицательных членов ряда ∑a_n также в их естественном порядке.

Ряды ∑P_n, ∑Q_n отличаются от рядов ∑p_n, ∑q_n только нулевыми членами и поэтому расходятся.

Мы построим такие последовательности {m_n}, {k_n}, что ряд

(25)

очевидно, являющийся перестановкой ряда ∑a_n, удовлетворяет условию (24).

Выберем последовательности вещественных чисел {α_n}, {β_n} так, что α_n→α, β_n→β, α_n<β_n.

Пусть m₁, k₁ - наименьшие из таких целых чисел, что

пусть m₂, k₂ - наименьшие из таких целых чисел, что

и т. д. Мы можем продолжить этот выбор, так как ряды ∑P_n и ∑Q_n расходятся.

Если через х_n, у_n обозначить частные суммы ряда (25), последние члены которых Р_mn, - Q_kn, то

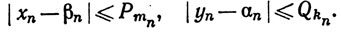
Мы видим, что x_n→β, у_n→α, так как Р_n→0 и Q_n→0 при n→∞.

Наконец, ясно, что никакое число, меньшее чем а или большее чем β, не может быть частичным пределом последовательности частных сумм ряда (25).

3.56. Теорема. Ряд ∑a_n сходится безусловно тогда и только тогда, когда он сходится абсолютно.

Доказательство. Допустим, что ряд ∑a_n сходится абсолютно. Пусть ∑a'_n - его перестановка, обладающая частными суммами s'_n. Для данного ε>0 существует целое число N, такое, что при m≥n≥N имеем

(26)

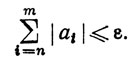
Выберем теперь р так, чтобы все целые числа 1, 2, ..., N содержались в множестве k₁, k₂, ...,k_p (мы используем обозначения из определения 3.52). Тогда при n>р числа а₁, ..., a_N в разности s_n - s'_n уничтожаются, так что |s_n - s'_n|<ε в силу (26). Значит, последовательность {s'_n} сходится к тому же пределу, что и {s_n}.

Теперь допустим, что ряд ∑a_n сходится неабсолютно. Если a_n = x_n + iy_n, где х_n и у_n вещественны, то |a_n|≤|x_n| + |y_n|. Поскольку ряд ∑|a_n| расходится, то расходится один из рядов ∑x_n и ∑y_n. Таким образом, один из рядов ∑x_n или ∑y_n сходится неабсолютно. Согласно теореме 3.55, имеется такая перестановка, что либо ряд ∑x'_n, либо ряд ∑y'_n расходится, так что и ряд ∑a'_n расходится.

Значит, ряд ∑a_n не является безусловно сходящимся.

Следующая теорема показывает, что в определении 3.53, не меняя его содержания, можно опустить фразу, заключенную в скобки.

3.57. Теорема.Если все перестановки ряда ∑a_n сходятся, то они сходятся к одной и той же сумме.

Доказательство. Либо ряд ∑a_n сходится абсолютно, и в этом случае ∑a_n сходится безусловно по теореме 3.56, либо ∑a_n не сходится абсолютно, и в этом случае по теореме 3.55 существует расходящаяся перестановка.