Сложение и умножение рядов

3.47. Теорема. Если ∑a_n = А и ∑b_n = В, то

Доказательство. Пусть

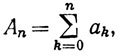
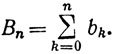
Тогда

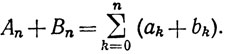
Ясно, что

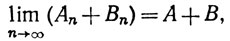
так как

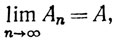
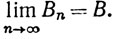
Доказательство второго утверждения даже проще.

Таким образом, два сходящихся ряда можно сложить почленно, и полученный ряд будет сходиться к сумме сумм этих двух рядов. Положение усложняется при рассмотрении произведения двух рядов. Сначала мы должны определить произведение. Это можно сделать разными способами; мы будем рассматривать так называемое произведение Коши.

3.48. Определение. Пусть заданы ряды ∑a_n и ∑b_n. Положим

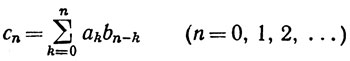
и назовем ряд ∑c_n произведением двух данных рядов.

Это определение можно объяснить следующим образом. Если, взяв два степенных ряда ∑a_nzⁿ и ∑b_nzⁿ, мы перемножим их подобно тому, как это делается в случае многочленов, и приведем подобные члены, то мы получим

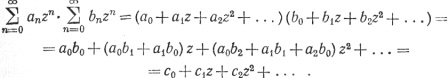
Полагая z = 1, мы приходим к данному выше определению.

3.49. Пример. Если

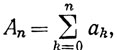
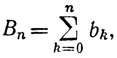
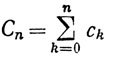
и А_n→А, В_n→В, то совсем не ясно, будет ли последовательность {С_n} сходиться к АВ, так как неверно, что С_n = А_nВ_n. Зависимость {С_n} от {А_n} и {В_n} очень сложна (см. доказательство теоремы 3.50). Сейчас мы покажем, что произведение двух сходящихся рядов может на самом деле расходиться.

Ряд

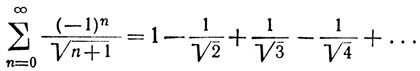
сходится (теорема 3.43). Составив произведение этого ряда с самим собой, мы получим

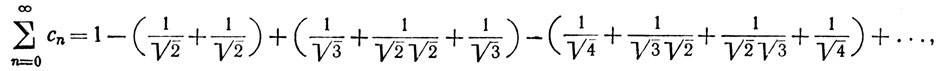
так что

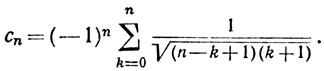
Так как

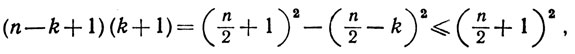
то мы имеем

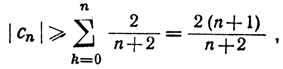
так что условие с_n→0, необходимое для сходимости ряда ∑c_n, не выполнено.

В связи со следующей теоремой, принадлежащей Мертенсу, заметим, что мы рассматривали в этом примере произведение двух неабсолютно сходящихся рядов.

3.50. Теорема.Допустим, что

(а) ряд 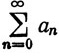сходится абсолютно,

(b)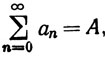

(c)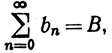

(d)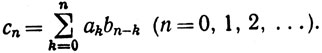

Тогда

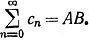
Это значит, что произведение двух сходящихся рядов сходится и сумма равна произведению сумм, если хотя бы один из этих двух рядов сходится абсолютно.

Доказательство. Положим

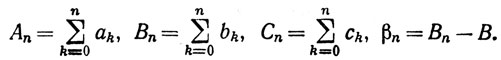
Тогда

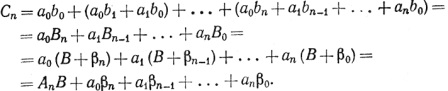
Положим

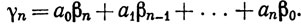
Мы хотим показать, что С_n→АВ. Достаточно показать, что

(21)

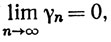
так как А_nB→АВ. Положим

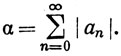
Именно здесь мы используем условие (а).] Пусть задано ε>0. В силу (с), β_n→0. Значит, можно выбрать N так, что 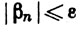при n≥N, и в этом случае

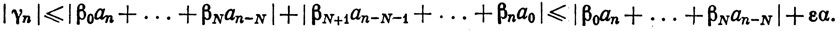
Оставляя N фиксированным и устремляя n к ∞, мы получим

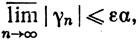
так как a_k→0 при k→∞. Отсюда и следует (21), так как ε произвольно.

Можно задать другой вопрос: обязательно ли сумма ряда ∑c_n, в том случае, когда он сходится, равна АВ? Абель показал, что ответ на этот вопрос-утвердительный.

3.51. Теорема.Если ряды ∑a_n, ∑b_n, ∑c_n сходятся соответственно к А, В, С и с_n = а₀b_n + ... + а_nb₀, то С = АВ.

Здесь не делается никаких предположений об абсолютной сходимости. Мы дадим простое доказательство (основанное на непрерывности степенных рядов) после теоремы 8.2.