Абсолютная сходимость

Говорят, что ряд ∑a_n сходится абсолютно, если сходится ряд ∑|a_n|.

3.45. Теорема.Если ряд ∑a_n сходится абсолютно, то он сходится.

Доказательство. Утверждение следует из неравенства

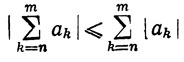
и из критерия Коши.

3.46. Замечания. Для рядов с положительными членами абсолютная сходимость - это то же самое, что сходимость.

Если ряд ∑a_n сходится, а ряд ∑|a_n| расходится, то говорят, что ряд ∑a_n сходится неабсолютно. Например, ряд

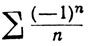
сходится неабсолютно (теорема 3.43).

Признак сравнения, так же как и признаки Даламбера и Коши, на самом деле есть признак абсолютной сходимости, и поэтому не может дать никакой информации о неабсолютно сходящихся рядах. Для работы с последними иногда можно пользоваться суммированием по частям. В частности, степенной ряд сходится абсолютно внутри круга сходимости.

Мы увидим, что с абсолютно сходящимися рядами можно обращаться совершенно так же, как с конечными суммами. Мы можем перемножать их почленно и переставлять слагаемые, не меняя суммы. Но для неабсолютно сходящихся рядов это уже неверно, и при действиях с ними нужна большая осторожность.