Суммирование по частям

3.41. Теорема.Пусть даны две последовательности {а_n}, {b_n}. Положим

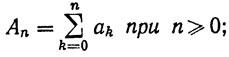
Тогда, если 0≤p≤q, то

(20)

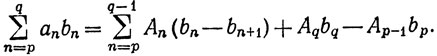
Доказательство. Имеем

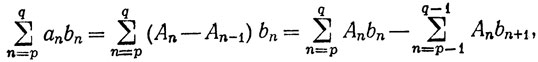
и последнее выражение справа, очевидно, равно правой части равенства (20).

Формула (20), так называемая формула суммирования

по частям, полезна при исследовании рядов вида ∑a_nb_n, в особенности, если последовательность {b_n} монотонна. Сейчас мы дадим ее приложения.

3.42. Теорема.Допустим, что

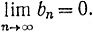
Тогда ряд ∑a_nb_n сходится.

Доказательство. Выберем М так, что |A_n|≤M при всех n. Для данного ε>0 существует целое число N, такое, что b_N≤(^ε/_2M). При N≤p≤q имеем

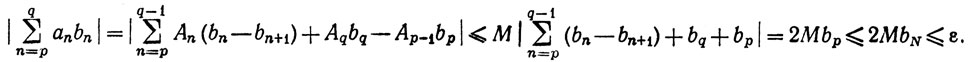
Сходимость следует теперь из критерия Коши. Заметим, что первое неравенство в написанной выше цепочке основано, конечно, на том, что b_n - b_n+1 ≥0.

3.43. Теорема.Допустим, что

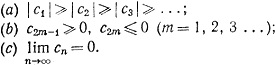
Тогда ряд ∑c_n сходится.

Ряд, для которого выполнено условие (b), называется "знакопеременным рядом"; сформулированная теорема была известна Лейбницу.

Доказательство. Применим теорему 3.42, положив a_n = (-1)ⁿ⁺¹,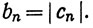

3.44. Теорема. Допустим, что радиус сходимости ряда ∑c_nzⁿ равен 1 и 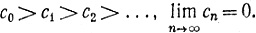Тогда ряд ∑c_nzⁿ сходится в каждой точке окружности 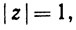за исключением, возможно, течки z = 1.

Доказательство. Положим a_n = zⁿ, b_n = c_n. Тогда выполнены условия теоремы 3.42, так как

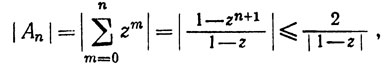
если 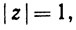z≠1.