
Степенные ряды
3.38. Определение. Пусть задана последовательность комплексных чисел {сn}. Ряд
(19)
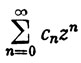
называется степенным рядом. Числа сn называются коэффициентами этого ряда; здесь z - комплексное число.
Вообще говоря, этот ряд сходится или расходится в зависимости от выбора числа z. Точнее, с каждым степенным рядом связан круг, так называемый круг сходимости, такой, что ряд (19) сходится, если z лежит внутри этого круга, и расходится, если z находится вне круга (чтобы охватить все случаи, мы должны рассматривать плоскость как внутренность окружности бесконечного радиуса, а точку-как окружность нулевого радиуса). Поведение ряда на окружности круга сходимости может быть гораздо более разнообразным, и его нельзя так просто описать.
3.39. Теорема.Пусть задан степенной ряд ∑cnzn. Положим
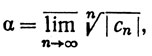
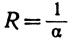
(если α = 0, то R = + ∞ ; если α = + ∞ , то R = 0). Тогда ряд ∑cnzn сходится, если 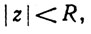 и расходится, если
и расходится, если 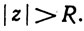
Доказательство. Положим an = cnzn и применим признак Коши. Имеем
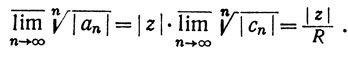
Замечание. Число R называется радиусом сходимости ряда ∑cnzn.
3.40. Примеры.(а) Для ряда ∑nnzn имеем R = 0.
(b) Для ряда 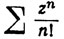 имеем R = +∞ (в этом случае проще применить признак Даламбера, чем признак Коши).
имеем R = +∞ (в этом случае проще применить признак Даламбера, чем признак Коши).
(c) Для ряда ∑zn имеем R = 1. Если 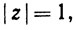 то ряд расходится, так как zn не стремится к 0 при n→∞.
то ряд расходится, так как zn не стремится к 0 при n→∞.
(d) Для ряда 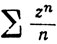 имеем R= 1. Этот ряд сходится во всех точках окружности круга сходимости, кроме z = 1. Это будет доказано в теореме 3.44.
имеем R= 1. Этот ряд сходится во всех точках окружности круга сходимости, кроме z = 1. Это будет доказано в теореме 3.44.
(e) Для ряда 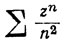 имеем R = 1. Этот ряд сходится во всех точках окружности круга сходимости согласно признаку сравнения, так как
имеем R = 1. Этот ряд сходится во всех точках окружности круга сходимости согласно признаку сравнения, так как 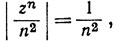 если
если 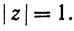
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'