
Другие признаки сходимости
3.33. Теорема (признак Коши). Пусть задан ряд ∑an. Положим 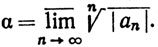 Тогда
Тогда
(a) если α<1, то ряд ∑an сходится;
(b) если α>1, то ряд ∑an расходится;
(c) существуют как сходящиеся, так и расходящиеся ряды, для которых а = 1.
Доказательство. Если а<1, то можно выбрать β так, что α<β<1, а целое число N - так, что 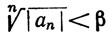 при n≥N [по теореме 3.17 (b)]. Иначе говоря, при n>N имеем
при n≥N [по теореме 3.17 (b)]. Иначе говоря, при n>N имеем
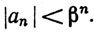
Ряд ∑βn сходится, так как 0<β<1. Сходимость ряда ∑an следует теперь из признака сравнения.
Если а>1, то, снова по теореме 3.17, существует последовательность {nk}, такая, что
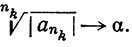
Значит, 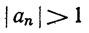 для бесконечного множества значений n, так что условие an→0, необходимое для сходимости ряда ∑an, не выполнено (теорема 3.23).
для бесконечного множества значений n, так что условие an→0, необходимое для сходимости ряда ∑an, не выполнено (теорема 3.23).
Чтобы доказать (с), рассмотрим ряды
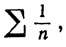
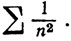
Для каждого из этих рядов α = 1 [по теореме 3.20 (с)], но первый расходится, а второй сходится.
3.34. Теорема (признак Даламбера). Ряд ∑an
(а) сходится, если 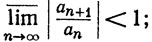
(b) расходится, если 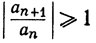 при n≥n0, где n0 - некоторое фиксированное число;
при n≥n0, где n0 - некоторое фиксированное число;
(c) существуют как сходящиеся, так и расходящиеся ряды, для которых
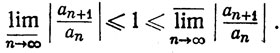
Доказательство. Если условие (а) выполнено, то можно найти β<1 и целое число N, такие, что
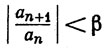
при n≥N. В частности,
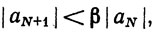
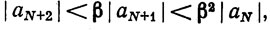
..............................................................

Это значит, что
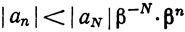
при n≥N; таким образом (а) следует из признака сравнения, так как ряд ∑βn сходится.
Если 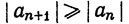 при n≥n0, то легко видеть, что условие an→0 не выполнено, откуда и следует (b).
при n≥n0, то легко видеть, что условие an→0 не выполнено, откуда и следует (b).
Чтобы доказать (с), мы снова рассмотрим ряды
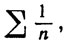
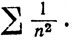
Для каждого из них мы имеем
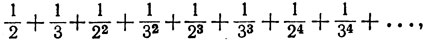
но первый расходится, а второй сходится.
3.35. Примеры. (а) Рассмотрим ряд
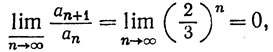
для которого
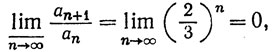
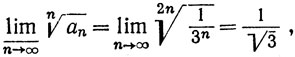
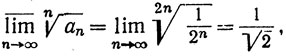
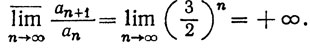
Признак Коши указывает на сходимость; признак Даламбера не позволяет сделать никаких заключений.
(b) То же самое верно в отношении ряда
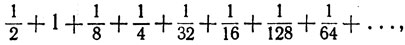
где
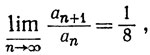
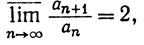
но
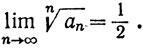
3.36. Замечания. Признак Даламбера, как правило, легче применять, чем признак Коши, так как обычно легче вычислять частные, чем корни n-й степени. Однако признак Коши сильнее в следующем смысле: когда признак Даламбера указывает на сходимость, то и признак Коши тоже указывает на сходимость; если же признак Коши не позволяет сделать никаких заключений, то и признак Даламбера тоже не позволяет сделать никаких заключений. Это следует из теоремы 3.37 и иллюстрируется приведенными выше примерами.
Ни один из этих двух признаков не является особенно тонким в отношении расходимости. В обоих расходимость выводится из того, что аn не стремится к нулю при n→∞.
3.37. Теорема. Для любой последовательности {сn} положительных чисел имеем
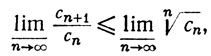
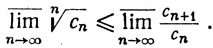
Доказательство. Мы докажем второе неравенство; доказательство первого совершенно аналогично. Положим
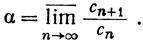
Если α = +∞, то доказывать нечего. Если α конечно, то выберем β>α. Существует целое N, такое, что
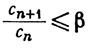
при n≥N. В частности, для любого p>0
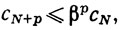
(k = 0, 1, ..., p-1)
Перемножая эти неравенства, мы получаем
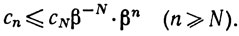
или
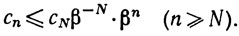
Значит,
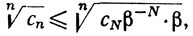
так что
(18)
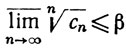
по теореме 3.20 (b). Поскольку неравенство (18) верно при любом β>α, имеем
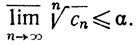
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'