Число е

3.30. Определение.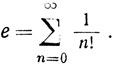

Здесь n = 1*2*3* ... *n, если n≥1, и 0! = 1.

Этот ряд сходится, так как

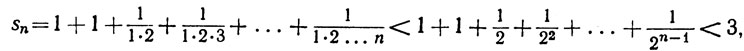
поэтому определение имеет смысл. На самом деле указанный ряд сходится очень быстро, и это позволяет нам вычислить е с большой точностью.

Интересно отметить, что е можно определить также при помощи другого предельного перехода; доказательство служит хорошей иллюстрацией того, как следует оперировать с пределами.

3.31. Теорема.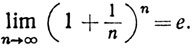

Доказательство. Пусть

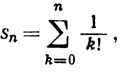
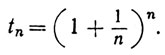
По теореме о биноме

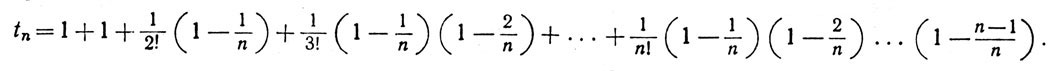
Значит, t_n≤s_n, так что

(14)

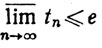
по теореме 3.19. Далее, если n≥m, то

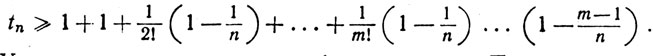
Устремим n к ∞, оставляя m фиксированным. Получим

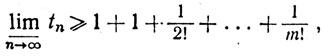
так что

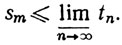
Устремляя m к ∞, мы окончательно получаем

(15)

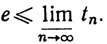
Теорема следует из (14) и (15).

Скорость, с которой сходится ряд 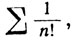можно оценить так: если s_n обозначает то же, что и выше, то

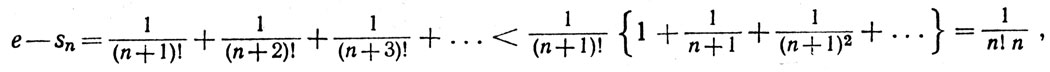
так что

(16)

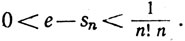
Таким образом, сумма s₁₀ приближает число е с ошибкой, меньшей 10^-7. Неравенство (16) представляет и теоретический интерес, так как оно позволяет очень легко доказать иррациональность числа е.

3.32. Теорема.Число е иррационально.

Доказательство. Допустим, что е рационально. Тогда e = ^p/_q, где р, q - положительные целые числа. В силу (16),

(17)

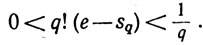
Согласно предположению, q!e - целое число. Число q!(е - s_q) также целое, поскольку

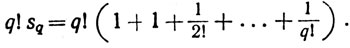
Так как q≥1, из (17) следует существование целого числа, заключенного между 0 и 1. Таким образом, мы добились противоречия.