Ряды с неотрицательными членами

Простейшим из всех таких рядов, по-видимому, является геометрическая прогрессия.

3.26. Теорема.Если 0≤х<1, то

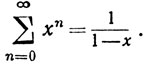
Если х≥1, то этот ряд расходится.

Доказательство. Если х≠1, то

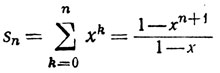
Устремляя n к ∞, мы получим требуемый результат. При х = 1 получается ряд

который, очевидно, расходится.

Во многих случаях, встречающихся в приложениях, члены ряда монотонно убывают. Поэтому следующая теорема Коши представляет особый интерес. Поразительная особенность утверждения теоремы состоит в том, что довольно "редкая" подпоследовательность последовательности {а_n} определяет сходимость или расходимость ряда ∑a_n.

3.27. Теорема. Допустим, что a₁≥a₂≥a₃≥...≥0. Тогда ряд 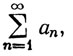сходится в том и только в том случае, когда сходится ряд

(7)

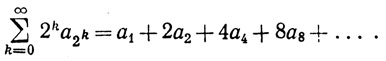
Доказательство. По теореме 3.24 достаточно установить ограниченность частных сумм. Пусть

При n<2^k имеем

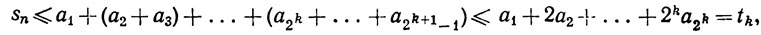
так что

(8)

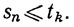
С другой стороны, при n>2^k

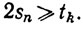
так что

(9)

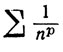
В силу (8) и (9), последовательности {s_n} и {t_k} или обе ограничены, или обе не ограничены.

Доказательство закончено.

3.28. Теорема.Ряд 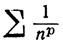сходится, если р>1, и расходится, если р≤1.

Доказательство. Если р≤0, то расходимость следует из теоремы 3.23. Если р>0, то применима теорема 3.27, и мы приходим к ряду

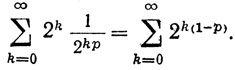
Но 2^(1-p)<1 тогда и только тогда, когда 1-р<0, и теорема вытекает из сопоставления с геометрической прогрессией (следует положить х = 2^1-p в теореме 3.26).

В качестве еще одного приложения теоремы 3.27 будет доказана следующая теорема.

3.29. Теорема. Если р>1, то ряд

(10)

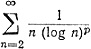
сходится; если р≤1, то этот ряд расходится.

Замечание. Символ log n обозначает логарифм числа n по основанию e (ср. упражнение 9, гл. 1); число е будет вскоре определено (см. определение 3.30). Мы начинаем ряд с n = 2, так как log 1 = 0.

Доказательство. Из монотонности логарифмической функции (которая более подробно будет рассматриваться в гл. 8) следует, что {log n} - возрастающая последовательность. Значит, последовательность 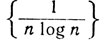убывает, и мы можем применить теорему 3.27 к ряду (10); это приводит к ряду

(11)

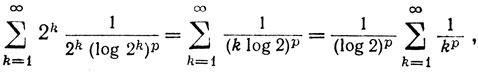
и теорема 3.29 следует из теоремы 3.28.

Эту процедуру, очевидно, можно продолжить. Например, ряд

(12)

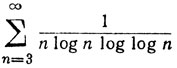
расходится, тогда как ряд

(13)

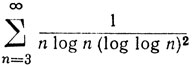
сходится.

Можно заметить, что члены ряда (12) очень мало отличаются от членов ряда (13). Однако один ряд сходится, а другой расходится. Продолжая процесс, который привел нас от теоремы 3.28 к теореме 3.29, а затем к (12) и (13), мы получим пары сходящихся и расходящихся рядов, члены которых отличаются даже меньше, чем члены рядов (12) и (13). Можно было бы предположить, что имеется некое предельное положение, "граница", по одну сторону которой лежат все сходящиеся, а по другую-все расходящиеся ряды, по крайней мере пока речь идет о рядах с монотонно убывающими членами. Конечно, это понятие "границы" совсем неясное. Однако мы хотим отметить следующее: как бы мы ни уточнили это понятие, такое предположение окажется неверным. Упражнения 11 (b) и 12 (b) могут служить иллюстрациями.

Мы не хотим вдаваться глубже в подобные вопросы теории сходимости и отсылаем читателя к главе IX, в особенности § 41, книги Кноппа^* (см. литературу).

^* (См. также Г. М. Фихтенгольц, Курс дифференциального и интегрального исчисления, т. II, М.- Л., 1948, п. 365.- Прим. перев.)