Ряды

В остальной части этой главы все рассматриваемые последовательности и ряды будут комплекснозначными, если явно не оговорено противное. В упражнении 15 предлагается распространить некоторые из следующих ниже теорем на ряды с членами из R^k.

3.21. Определение. Пусть задана последовательность {а_n}. Мы будем обозначать сумму a_p + a_p+1 + ... +a_q (p≤g) через 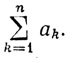Последовательности {а_n} мы сопоставим последовательность {s_n}, где

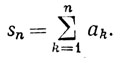
Символ

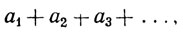
или, короче,

(4)

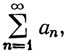
мы будем называть бесконечным рядом или просто рядом. Числа s_n называются частными суммами этого ряда. Если последовательность {s_n} сходится к s, то мы будем говорить, что ряд сходится, и будем писать

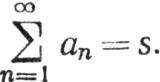
Число s называется суммой этого ряда, но необходимо ясно понимать, что s является пределом последовательности сумм, а не получается простым сложением.

Если последовательность {s_n} расходится, то говорят, что ряд расходится.

Иногда для удобства обозначений мы будем рассматривать ряды вида

(5)

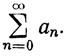
Часто мы будем вместо (4) или (5) писать просто ∑a_n.

Ясно, что каждую теорему о последовательностях можно сформулировать на языке рядов (полагая a₁ = s₁ и a_n = s_n - s_n-1 при n>1), и обратно. Но тем не менее полезно различать эти понятия.

Критерий Коши (теорему 3.11) можно сформулировать в следующем виде.

3.22. Теорема.Ряд ∑a_n сходится тогда и только тогда, когда для любого ε>0 существует целое N, такое, что

(6)

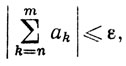
если m≥n≥N.

В частности, при m = n неравенство (6) превращается в неравенство

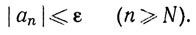
Иными словами, справедлива следующая теорема.

3.23. Теорема. Если ряд ∑a_n сходится, то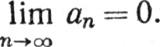

Однако условие а_n→0 не достаточно для того, чтобы обеспечить сходимость ряда ∑a_n. Например, ряд

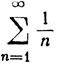
расходится; за доказательством мы отсылаем к теореме 3.28.

Теорема 3.14 о монотонных последовательностях также имеет очевидный аналог для рядов.

3.24. Теорема.Ряд неотрицательных^* членов сходится тогда и только тогда, когда его частные суммы образуют ограниченную последовательность.

^* (Выражение "неотрицательный" всегда относится к вещественным числам.)

Теперь мы обратимся к признаку сходимости другой природы-к так называемому "признаку сравнения".

3.25. Теорема.(а) Если 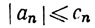при n≥N₀, где N₀ - некоторое фиксированное целое, и если ряд ∑c_n сходится, то и ряд ∑a_n сходится.

(b) Если a_n≥d_n≥0 при n≥N₀ и если ряд ∑d_n расходится, то и ряд ∑a_n расходится.

Заметим, что признак (b) применим только к рядам с неотрицательными членами а_n.

Доказательство. Согласно критерию Коши, для данного ε>0 существует N≥N₀, такое, что при m≥n≥N имеем

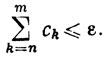
Значит,

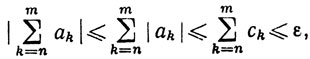
и (а) доказано.

Далее, (b) следует из (а), так как если ряд ∑a_n сходится, то и ряд ∑d_n должен сходиться (заметим, что (b) следует также из теоремы 3.24).

Этот признак сравнения очень полезен; чтобы успешно применять его, мы должны освоиться с некоторым набором рядов с неотрицательными членами, заведомо сходящихся или расходящихся.