Некоторые специальные последовательности

Теперь мы вычислим пределы некоторых часто встречающихся последовательностей. Все доказательства будут основаны на следующем замечании: если 0≤x_n≤s_n при n≥N, где N - некоторое фиксированное число, и если s_n→0, то х_n→0.

3.20. Теорема.(а) Если р>0, то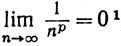

(b) Если р>0, то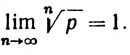

(c)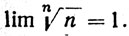

(d) Если p>0 и α - вещественное число, то

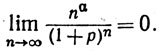
(e) Если 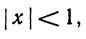то

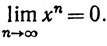
¹ (Смысл символа n^p не был до сих пор определен, то же относится и к n^α в пункте (d); указания на способ определения степени с любым вещественным показателем содержатся в упражнении 7 к гл. 1.- Прим. перев.)

Доказательство. (а) Возьмем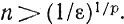

(b) Если р>1, то положим 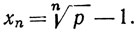Тогда x_n>0 и, согласно теореме о биноме,

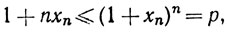
так что

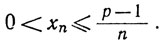
Значит, х_n→0. Если р = 1, то (b) тривиально; если 0<p<11, то результат получается переходом к обратным числам.

(c) Положим 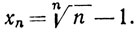Тогда x_n≥0 и, согласно теореме о биноме,

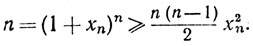
Значит,

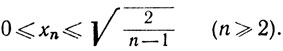
(d) Пусть k - такое целое число, что k>α, k>0. Для n≥2k имеем

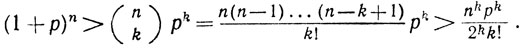
Значит,

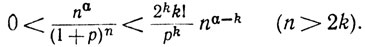
Поскольку α - k <0, имеем n^α-k→ 0 в силу (а).

(e) Возьмем α = 0 в (d).