
Верхний и нижний пределы
3.15. Определение. Пусть {sn} - последовательность вещественных чисел, обладающая следующим свойством: для любого вещественного М существует целое N, такое, что при n≥N мы имеем sn≥M. Тогда мы пишем
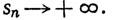
Аналогичным образом, если для любого вещественного числа М существует целое N, такое, что при n≥N мы имеем sn≤M, то мы пишем
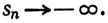
Следует отметить, что мы теперь используем символ → (введенный в определении 3.1) для некоторых типов расходящихся последовательностей, так же как и для сходящихся последовательностей, но что определения сходимости и предела, данные в п. 3.1, никоим образом не меняются.
3.16. Определение. Пусть {sn} - последовательность вещественных чисел. Пусть Е - множество чисел х (в расширенной системе вещественных чисел), таких, что snk→x для некоторой подпоследовательности {snk}. Это множество Е содержит все частичные пределы, определенные в п. 3.5, и, возможно, числа +∞, -∞.
Вспомним теперь определения 1.34 и 1.40 и положим
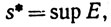
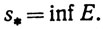
Числа s*, s* называются верхним и нижним пределами последовательности {sn}; мы используем обозначения
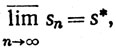
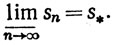
3.17. Теорема.Пусть {sn} - последовательность вещественных чисел. Пусть Е и s* имеют тот же смысл, что и в определении 3.16. Тогда s* обладает следующими свойствами:
(a) s*∈E;
(b) если x>s*, то существует целое N, такое, что при n≥N имеем sn<x. Более того, s* - единственное число, обладающее свойствами (а) и (b).
Конечно, аналогичный результат верен для s*.
Доказательство. Если s* = +∞, то множество Е не ограничено сверху; значит, последовательность {sn} не ограничена сверху и существует подпоследовательность {snk}, такая, что snk→+∞.
Если s* - вещественное число, то множество Е ограничено сверху и существует по крайней мере один частичный предел, поэтому (а) следует из теорем 3.7 и 2.28.
Если s* = -∞, то Е содержит только один элемент, а именно -∞, и не существует ни одного частичного предела. Значит, для любого вещественного М неравенство sn>M может выполняться лишь для конечного множества значений n, так что sn→-∞.
Тем самым (а) установлено во всех случаях.
Чтобы доказать (b), допустим, что существует число x>s*, такое, что sn≥x для бесконечного множества значений n. В этом случае существует число у∈Е, такое, что y≥x>s*, а это противоречит определению s*.
Таким образом, s* удовлетворяет условиям (а) и (b).
Для доказательства единственности допустим, что существуют два числа р и q, удовлетворяющие условиям (а) и (b), и допустим, что р<q. Выберем х таким, что p<x<q. При n≥N имеем sn<x, так как р удовлетворяет условию (b). Но тогда q не может удовлетворять условию (а).
3.18. Примеры, (а) Пусть {sn} - последовательность, содержащая все рациональные числа. Тогда каждое вещественное число является частичным пределом и
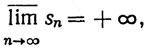
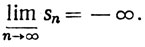
(b) Пусть 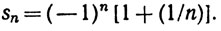 Тогда
Тогда
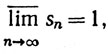
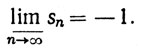
(c) Для последовательности {sn} вещественных чисел 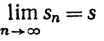 тогда и только тогда, когда
тогда и только тогда, когда
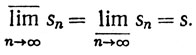
Мы закончим этот раздел одной полезной теоремой, доказательство которой совсем тривиально.
3.19. Теорема. Если sn≤tn при n≥N, где N фиксировано, то
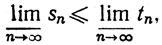
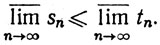
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'