Последовательности Коши

3.8. Определение. Последовательность {р_n} в метрическом пространстве X называется последовательностью Коши(фундаментальной последовательностью, последовательностью, к сходящейся в себе), если для любого ε>0 существует целое N, такое, что d(р_n, р_m)<ε при n≥N и m≥N.

При рассмотрении последовательностей Коши, а также в других ситуациях, которые возникнут позднее, окажется полезным следующее геометрическое понятие.

3.9. Определение. Пусть Е - подмножество метрического пространства X, и пусть S - множество всех вещественных чисел вида d(p, q), где р∈Е и q∈E. Диаметром множества Е называется число sup S. Это число обозначается diam E.

Если {р_n} - последовательность в X, a E_N состоит из точек p_N, p_N+1, p_N+2, ..., то из двух последних определений ясно, что {р_n} - последовательность Коши тогда и только тогда, когда

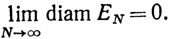
3.10. Теорема, (а) Если 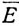есть замыкание множества Е в метрическом пространстве X, то

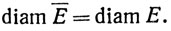
(b) Если {К_n} - последовательность компактных множеств в X, такая, что K_n⊃K_n+1 (n = 1, 2, 3, ...), и если

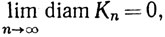
то 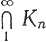состоит ровно из одной точки.

Доказательство. (а) Ясно, что

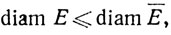
так как Е⊂.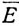

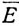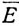Зафиксируем число ε>0 и выберем р∈, q∈. По определению множества 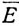, в Е содержатся точки p', q', такие, что d(p, p')<ε, d(q, q')<ε. Значит,

Следовательно,

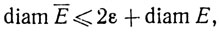
и так как ε произвольно, утверждение (а) доказано.

(b) Положим 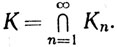По теореме 2.36, К непусто. Если К содержит более одной точки, то diam K> 0. Но при каждом n мы имеем К_n⊃К, так что diam K_n ≥ diam К. Это противоречит предположению, что diam K_n→0.

3.11. Теорема, (а) Всякая сходящаяся последовательность в метрическом пространстве X является последовательностью Коши.

(b) Всякая последовательность Коши в R^k сходится.

Замечание. Разница между определением сходящейся последовательности и определением последовательности Коши состоит в том, что в первое определение в явном виде входит предел, в то время как во второе определение он не входит. Таким образом, теорема 3.11 (b) позволяет нам решить, сходится или нет данная последовательность, даже если мы не знаем предела, к которому она может сходиться.

То (содержащееся в теореме 3.11) утверждение, что последовательность в R^k сходится тогда и только тогда, когда она является последовательностью Коши, обычно называют критерием сходимости Коши.

Доказательство, (а) Если 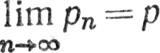и ε>0, то существует целое N, такое, что 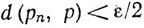при n≥N. Значит, если n≥N и m≥N, то

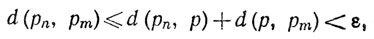
так что {р_n} - последовательность Коши.

(b) Допустим, что {х_n} - последовательность Коши в R^k. Пусть E_N - множество, состоящее из точек x_N, x_N+1, x_N+2, ... и пусть _N - замыкание множества E_N. По определению 3.9 и по теореме 3.10 (а) мы имеем

(3)

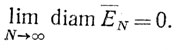
В частности, множества 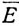_N ограничены. Кроме того, они замкнуты. (Это следует из упражнения 4, гл. 2. Вот короткое доказательство: если х∉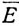_N, то х∉E_N, и х не является предельной точкой множества E_N; поэтому некоторая окрестность V точки х не пересекается с E_N. Никакая точка окрестности V не принадлежит E_N, так как множество V открыто; следовательно, дополнение множества E_N открыто.) Значит, каждое множество 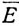_N компактно (теорема 2.41). Кроме того, E_N⊃E_N+1 так что 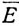_N⊃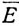_N+1. По теореме 3.10 (b) существуетvединственная точка x∈R^k принадлежащая каждому множеству 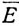_N.

Пусть задано число ε>0. В силу (3) имеется целое N₀, такое, что diam 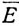_N<ε, если N≥N_n. Поскольку х&38712;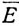_N, это значит, что 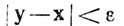при всех у&38712;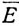_N, а поэтому и при всех y∈E_N. Иными словами, если n≥N₀, то 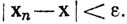Но это означает в точности, что х_n→х, и доказательство закончено.

3.12. Определение. Метрическое пространство X, в котором каждая последовательность Коши сходится, называется полным. Поэтому теорему 3.11 (b) можно сформулировать так: R^kv-vполное метрическое пространство. Примером неполного метрического пространства служит пространство всех рациональных чисел с расстоянием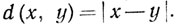

Теорема 3.2 (с) и пример (d) из п. 3.1 показывают, что сходящиеся последовательности ограничены, но ограниченные последовательности в R^k не обязательно сходятся. Однако имеется один важный случай, когда сходимость равносильна ограниченности. Так обстоит дело с монотонными последовательностями в R¹.

3.13. Определение. Последовательность {s_n} вещественных чисел называется

(a) монотонно возрастающей, если s_n≤s_n+1, (n = 1, 2, 3, ...);

(b) монотонно убывающей, если s_n≥s_n+1 (n = 1, 2, 3, ...).

Класс монотонных последовательностей состоит из возрастающих и убывающих последовательностей.

3.14. Теорема.Монотонная последовательность {s_n} сходится в том и только в том случае, когда она ограничена.

Доказательство. Допустим, что s_n≤s_n+1 (в другом случае доказательство аналогично). Пусть Е - множество значений последовательности {s_n}. Если последовательность {s_n} ограничена, то пусть s - верхняя грань множества Е. Тогда

Для любого ε>0 существует целое N, такое, что s-ε<s_N≤s, так как иначе s-ε было бы верхней границей множества Е. Поскольку последовательность {s_n} возрастает, то при n≥N имеем

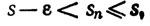
откуда следует, что {s_n} сходится (к s).

Обратное следует из теоремы 3.2 (с).