Подпоследовательности

3.5. Определение. Пусть задана последовательность {р_n}. Рассмотрим последовательность {n_k) положительных целых чисел, такую, что n₁<n₂<n₃<... . Тогда последовательность {р_ni} называется подпоследовательностью последовательности {р_n}. Если последовательность {р_ni} сходится, то ее предел называется частичным пределом последовательности {р_n}.

Ясно, что последовательность {р_n} сходится к р тогда и только тогда, когда всякая ее подпоследовательность сходится к р. Мы предоставляем читателю провести детальное доказательство.

3.6. Теорема.Всякая ограниченная последовательность в R^k содержит сходящуюся подпоследовательность.

Доказательство. Пусть Е - множество значений ограниченной последовательности {х_n} в R^k. Если Е конечно, то существуют по крайней мере одна точка х множества Е и последовательность {n_i} (n₁<n₂<n₃<...), такие, что

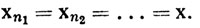
Полученная таким образом подпоследовательность, очевидно, сходится.

Если множество Е бесконечно, то оно имеет предельную точку x∈R^k (теорема 2.42). Выберем n₁ так, что 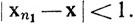Выбрав n₁, ..., n_i-1, мы получим, по теореме 2.22, что существует целое n_i>n_i-1, такое, что 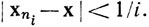Построенная таким образом подпоследовательность сходится к х.

3.7. Теорема.Частичные пределы последовательности {р_n} в метрическом пространстве X образуют замкнутое множество в X.

Доказательство. Пусть Е - множество значений последовательности {р_n}, а Е^* - множество всех частичных пределов этой последовательности. Допустим, что q - предельная точка множества Е^*. Чтобы показать, что q∈E^*, достаточно, по теореме 3.2 (d), показать, что q - предельная точка множества Е.

Пусть задано число ε>0. Поскольку q - предельная точка множества Е^*, имеется точка р∈Е^*, такая, что

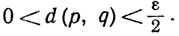
Так как р∈Е^*, то при некотором р_n имеем

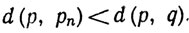
Значит, p_n ≠q и

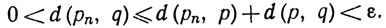
Поскольку p_n∈E, отсюда следует, что q - предельная точка множества Е, и доказательство закончено.