Сходящиеся последовательности

3.1. Определение. Последовательность {р_n} в метрическом пространстве X называется сходящейся, если существует точка р∈Х, обладающая следующим свойством: для каждого ε>0 существует целое число N, такое, что при n≥N имеем d (р_n, р)<ε (здесь d обозначает расстояние в X).

В этом случае мы будем говорить также, что последовательность {р_n} сходится к р или что р - предел последовательности {р_n} [см. теорему 3.2 (b)], и будем писать р_n→р или

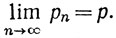
Если последовательность {р_n} не сходится, то говорят, что она расходится.

Полезно отметить, что наше определение "сходящейся последовательности" зависит не только от {р_n}, но и от X; например, последовательность {¹/_n} сходится в R¹{к 0), но не сходится в множестве всех положительных вещественных чисел [когда d(x, у) = |x - y|]. В тех случаях, когда возможна путаница, мы будем более точными и будем говорить отчетливо "сходится в X" вместо "сходится".

Напомним, что множество всех точек р_n (n = 1, 2, 3, ...) есть множество значений последовательности {р_n}. Множество значений последовательности может быть конечным или бесконечным. Последовательность называется ограниченной, если множество ее значений ограничено.

Для примера рассмотрим следующие последовательности комплексных чисел (при этом X = R²).

(a) Если s_n = ¹/_n, то 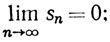множество значений бесконечно, и последовательность ограничена.

(b) Если s_n = n², то последовательность {s_n} не ограничена, расходится, а множество ее значений бесконечно.

(c) Если s_n = 1 + [^(-1)n/_n], то последовательность {s_n} сходится к 1, ограничена, а множество ее значений бесконечно.

(d) Если s_n = iⁿ, то последовательность {s_n} расходится, ограничена, а множество ее значений конечно.

(e) Если s_n = 1 (n = 1,2, 3, ...), то {s_n} сходится к 1, ограничена, а множество ее значений конечно.

Сформулируем теперь некоторые важные свойства сходящихся последовательностей в метрических пространствах.

3.2. Теорема.Пусть {р_n} - последовательность в метрическом пространстве X.

(d) Если Е⊂Х и если р - предельная точка множества Е, то существует последовательность {р_n} элементов множества Е, такая, что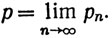

Доказательство. (а) Допустим, что р_n→р, и пусть V - окрестность точки р. Для некоторого ε>0 из условий d(p, q)<ε, q∈X, следует, что q∈V. Этому ε соответствует N, такое, что из неравенства n≥N следует, что d (р_n, р)<ε. Таким образом, неравенство n≥N влечет за собой включение р_n∈V.

Обратно, допустим, что каждая окрестность точки р содержит все точки р_n, кроме конечного их числа. Зификсируем ε>0, и пусть V - множество всех q∈X, таких, что d(p, q)<ε. По предположению, существует N (соответствующее этой окрестности V), такое, что p_n∈V, если n≥N. Таким образом, d(p_n, p)<ε, если n≥N; значит, р_n→р.

(b) Пусть задано число ε>0. Существуют целые числа N, N', такие, что

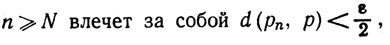
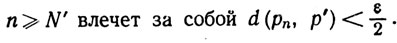
Значит, если n≥max(N, N'), то

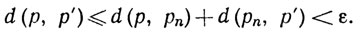
Поскольку число ε было произвольным, мы заключаем отсюда, что d(p, р') = 0.

(c) Допустим, что р_n→р. Тогда существует целое N, такое, что при n>N имеем d (р_n, р)<1. Положим

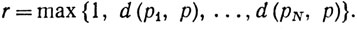
Тогда d(p_n, p)≤r при n = 1, 2, 3,....

(d) Для каждого положительного целого n существует точка р_n∈Е, такая, что d(p_n, р)<¹/_n. Для данного ε>0 выберем N так, что N_ε>1. Если n>N, то d(p_n, p)<ε. Значит, р_n→р.

Доказательство закончено.

Для последовательностей в R^k мы можем изучать соотношения между сходимостью, с одной стороны, и алгебраическими операциями, с другой. Сначала мы рассмотрим последовательности комплексных чисел.

3.3. Теорема.Допустим, что {s_n}, {t_n} - комплексные последовательности и 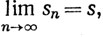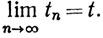Тогда

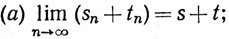
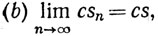
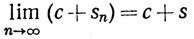
для любого числа c;

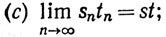
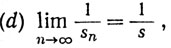
если только s_n ≠ 0 (n = 1, 2, 3, ...) и s≠0.

Доказательство.(а) Для данного ε>0 существуют целые N₁, N₂, такие, что

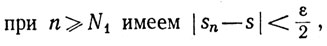
Если N = max(N₁, N₂), то при n≥N получим

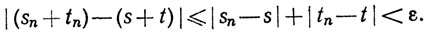
Тем самым (а) доказано. Доказательство утверждения (b) тривиально.

(с) Воспользуемся тождеством

(1)

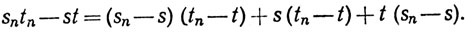
Для данного ε>0 существуют целые N₁, N₂, такие, что

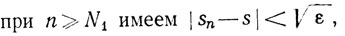
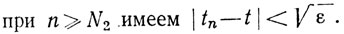
Если мы возьмем N = max(N₁, N₂), то при n≥N получим

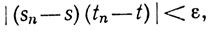
откуда

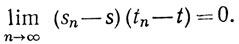
Применив теперь (а) и (b) к тождеству (1), мы заключаем, что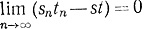

(d) Выбрав m так, что 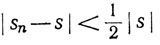при n≥m, мы видим, что

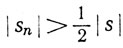
(n≥m)

Для данного ε>0 существует целое N>m, такое, что при n≥N имеем

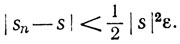
Отсюда при n≥N получаем

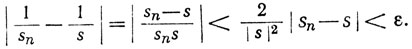
3.4. Теорема,(а) Допустим, что x_n∈R^k (n = 1, 2,3,...) и

x_n = (α_1,n, ..., α_{k, n}).

Последовательность {x_n} сходится к х = (α₁, ..., α_k) тогда а только тогда, когда

(2)

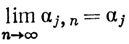
(1≤j≤k)

(b) Допустим, что {х_n}, {у_n} - последовательности в R^k, {β_n} -последовательность вещественных чисел и х_n→х, у_n→у, β_n→β. Тогда

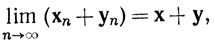
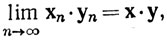
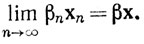
Доказательство. Если х_n→х, то равенство (2) выполняется в силу неравенств

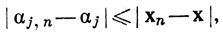
вытекающих непосредственно из определения нормы в R^k.

Обратно, если (2) выполнено, то каждому ε>0 соответствует целое N, такое, что при n≥N имеем

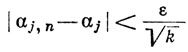
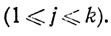
Значит, при n≥N получаем

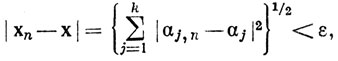
откуда х_n→х. Тем самым (а) доказано.

Утверждение (b) следует из (а) и теоремы 3.3.