Связные множества

2.45. Определение. Множество Е в метрическом пространстве X называется связным, если не существует двух открытых множеств А и В пространства X, таких, что пересечение А∩В пусто, пересечения А∩Е и В∩Е не пусты и Е⊂А∪В.

Это определение похоже на определение компактности, поскольку на самом деле оно не зависит от объемлющего пространства X, т. е. при замене слова "связное" словами "связное относительно X" в предыдущем абзаце выполняется следующее утверждение: Е связно относительно X в том и только в том случае, когда Е связно относительно Е.

Таким образом, имеет смысл говорить о связных пространствах (ср. с замечаниями, следующими за формулировкой теоремы 2.33): пространство связно, если оно не является объединением двух непустых непересекающихся открытых множеств.

Первая часть утверждения, набранного выше курсивом, почти тривиальна: если Е не является связным относительно X, то существуют множества А и В, обладающие свойствами, указанными в определении, ичрассмотрение множеств А∩Е и В∩Е показывает, что Е не связно относительно Е (ср. с теоремой 2.30). Обратное вытекает из следующего результата.

2.46. Теорема.Пусть X - метрическое пространство, Е⊂Х и E = G∪H, где G и Н - непересекающиеся непустые множества, открытые относительно Е. Тогда существуют непересекающиеся открытые множества А и В в X, такие, что G = A∩Е, Н = В∩Е.

Доказательство. Каждой точке р∈G соответствует число δ_p>0, такое, что из соотношений q∈E, d(p, q)<δ_p следует включение q∈G, так как множество G открыто относительно Е.

Аналогичным образом, каждой точке q∈H соответствует число δ_q>0, такое, что из соотношений р∈Е, d(p, q)<δ_q следует включение р∈H. Значит, если p∈G, q∈H, то оба эти неравенства не выполняются, так что

(25)

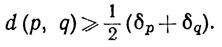
При p∈G, q∈H пусть V_p обозначает множество всех х∈Х, таких, что 2d(p, x)<δ_p, и пусть W_q - множество всех х∈Х, таких, что 2d(q, х)∈δ_q. Если некоторое множество V_p имеет общую точку х с некоторым W_q, то

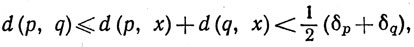
что противоречит неравенству (25).

Таким образом, каждое V_p не пересекается ни с одним W_q, и если мы положим

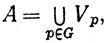
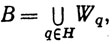
то мы получим множества с требуемыми свойствами.

2.47. Теорема.Подмножество Е вещественной прямой R¹ связно тогда и только тогда, когда Е обладает следующим свойством: если х∈Е, у∈Е и x<z<y, то и z∈E.

Доказательство. Допустим, что это условие не выполняется для некоторых чисел х, у, z, т. е. х∈Е, у∈Е, x<z<y, но z∉Е. Если А есть множество всех α<z, а B - множество всех β>0, то определение 2.45 показывает, что Е не связно.

Чтобы доказать обратное, допустим, что Е не связно. Тогда существуют точки х∈Е, у∈Е, х<<у, и открытые непересекающиеся множества А и В в R>¹, такие, что х∈А, у∈В и Е⊂A∪B. Пусть

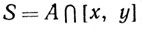
и z = sup S.

Ввиду того что у∈В и В открыто, имеем z<y. Таким образом, если z∈A, то из того, что А открыто, следует, что z не является верхней границей множества S. Значит, z∉А.

Ввиду того что х∈А и А открыто, имеем x<z. Таким образом, если z∈B, то из того, что В открыто, следует, что z не является верхней гранью множества S. Значит, z∉B.

Но так как Е⊂A∪В, то z∉Е, и доказательство закончено.

Следствие.Множество Е в R¹ связно тогда и только тогда, когда Е - одно из следующих множеств (где а и b - вещественные числа, а≤b):

К какому из этих типов принадлежит множество Е, зависит от того, конечны или нет inf E и sup E и принадлежат ли они множеству Е.

Столь же простой характеристики связных множеств на плоскости, например, не существует.