Совершенные множества

2.43. Теорема.Пусть Р - непустое совершенное множество в R^k. Тогда Р несчетно.

Доказательство. Поскольку множество Р имеет предельные точки, оно должно быть бесконечным. Допустим, что Р счетно, и обозначим точки множества Р через х₁, х₂, х₃, ... .

Мы построим последовательность окрестностей {V_n} следующим образом.

Пусть V₁ - какая-нибудь окрестность точки х₁. Если V₁ состоит из всех y∈R^k, таких, что 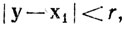то соответствующая замкнутая окрестность V₁ есть по определению множество всех у∈R^k, таких, что 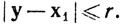(Как и в теореме 2.21, легко доказать, что дополнение множества 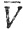₁ открыто. Значит, замкнутые окрестности замкнуты.)

Допустим, что окрестность V_n построена так, что множество V_n∪P непусто. Поскольку каждая точка множества Р есть предельная точка этого множества, существует окрестность V_n+1, такая, что (i) 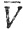_n+1⊂V_n, (ii) x_n∉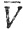_n+1, (iii) множество V_n+1∩P непусто. В силу (iii), V_n+1 удовлетворяет предположению индукции, и построение может быть продолжено.

Положим 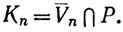Будучи ограниченным и замкнутым, множество 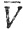_n компактно. Ни одна точка множества Р не лежит в 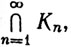так как х_n∉K_n+1. Отсюда следует, что множество 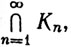пусто, так как К_n⊂P. Но ведь каждое множество К_n непусто в силу (iii) и К_n⊂K_n+1 в силу (i). Это противоречит следствию из теоремы 2.36.

Следствие.Каждый сегмент [a, b] (a<b) несчетен. Множество всех вещественных чисел несчетно.

2.44. Канторово множество. Пример, к построению которого мы переходим, показывает, что в R¹ существуют совершенные множества, не содержащие никакого интервала.

Пусть E₀ есть сегмент 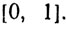Удалим из него интервал 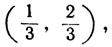и пусть E₁ - объединение сегментов

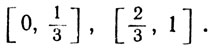
Удалим средние трети этих сегментов, и пусть E₂ -объединение сегментов

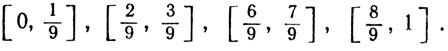
Продолжая таким образом, мы получим последовательность компактных множеств Е_n, таких, что

(а) E₁⊂E₂⊂E₃⊂...;

(b) Е_n есть объединение 2ⁿ сегментов, длина каждого из которых равна 3^-n.

Множество 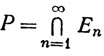называется множеством Кантора. Множество Р, очевидно, компактно, и теорема 2.36 показывает, что Р непусто.

Никакой интервал вида

(24)

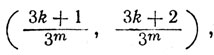
где k и m - положительные целые числа, не имеет общих точек с Р. Значит, Р не содержит никакого интервала, ибо каждый интервал (α, β) содержит интервал вида (24), если

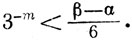
Чтобы показать, что Р совершенно, достаточно показать, что Р не содержит изолированных точек. Пусть х∈Р и пусть S - какой-нибудь интервал, содержащий х. Пусть I_n - сегмент множества Е_n, содержащий х. Выберем достаточно большое n, такое, что I_n⊂S. Пусть х_n - тот конец сегмента I_n, для которого x_n≠x.

Из построения множества Р следует, что х_n∈Р. Значит, х есть предельная точка множества Р, и множество Р совершенно.

Одно из самых интересных свойств множества Кантора состоит в том, что оно доставляет нам пример несчетного множества меры нуль (понятие меры будет обсуждаться в гл. 10).