Компактные множества

2.31. Определение. Открытым покрытием множества Е в метрическом пространстве X мы будем называть семейство {G_α} открытых подмножеств пространства X, такое, что Е⊂.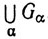

2.32. Определение. Подмножество К метрического пространства X называется компактным, если каждое открытое покрытие множества К содержит конечное подпокрытие.

Говоря точнее, требование состоит в том, что если {G_α} - открытое покрытие множества К, то имеется конечное число индексов α₁, ..., α_n, таких, что

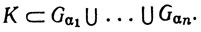
Понятие компактности имеет большое значение в анализе, особенно в связи с непрерывностью (гл. 4).

Ясно, что каждое конечное множество компактно. Существование широкого класса бесконечных компактных множеств в R^k будет следовать из теоремы 2.41.

Мы заметили ранее (в п. 2.29), что если E⊂Y⊂X, то множество Е может быть открытым относительно Y, не будучи открытым относительно X. Свойство множества Е быть открытым зависит, таким образом, от пространства, в которое оно погружено. То же верно и в отношении свойства множества быть замкнутым.

Однако, как мы увидим, компактность - более удобное понятие. Чтобы сформулировать следующую теорему, мы будем говорить временно, что множество К компактно относительно X, если выполнены требования определения 2.32.

2.33. Теорема.Допустим, что К⊂Y⊂X. Множество К компактно относительно X в том и только в том случае, когда оно компактно относительно Y.

В силу этой теоремы мы сможем во многих ситуациях рассматривать компактные множества как метрические пространства сами по себе, не обращая никакого внимания на объемлющее пространство. В частности, хотя почти бессмысленно говорить об открытых пространствах или о замкнутых пространствах (каждое метрическое пространство X служит открытым подмножеством самого себя и замкнутым подмножеством самого себя), имеет смысл говорить о компактных метрических пространствах.

Доказательство. Предположим, что множество К компактно относительно X; пусть {V_α} - семейство множеств, открытых относительно Y, такое, что K⊂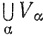. По теореме 2.30 при каждом α существует множество G_α, открытое относительно X, такое, что V_α = Y∩G_α; поскольку К компактно относительно X, мы имеем

(22)

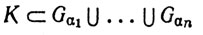
при некотором выборе конечного числа индексов α₁, ..., α_n.

Так как К⊂Y, то из (22) следует, что

(23)

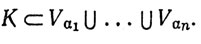
Тем самым доказано, что множество К компактно относительно Y.

Обратно, допустим, что К компактно относительно Y. Пусть {G_α} - семейство открытых подмножеств пространства X, покрывающее К. Положим V_α = Y∩G_α. Тогда включение (23) будет выполнено при некотором выборе α₁, ..., α_n; так как V_α⊂G_α, то (22) следует из (23).

Доказательство закончено.

2.34. Теорема.Компактные подмножества метрических пространств замкнуты.

Доказательство. Пусть К - компактное подмножество метрического пространства X. Мы докажем, что дополнение множества К есть открытое подмножество пространства X.

Предположим, что р∈X, р∉К. Если q∈К, то пусть V_q и W_q - окрестности соответственно точек р и q радиуса, меньшего ½d(p, q) [см. определение 2.20 (а)].

Ввиду того что К - компактно, найдется конечный набор точек q₁, ..., q_n, принадлежащих множеству К. таких, что

Если V = V_q1∩...∩V_qn , то V - окрестность точки р, не пересекающаяся с W. Значит, V⊂K^c, так что р - внутренняя точка множества К^с. Теорема доказана.

2.35. Теорема.Замкнутые подмножества компактных множеств компактны.

Доказательство. Допустим, что F⊂К⊂X, множество F замкнуто (относительно X), а K - компактно. Пусть {V_α} - открытое покрытие множества F. Если присоединить множество F^c к {V_α}, то мы получим открытое покрытие Ω множества К. Поскольку К компактно, существует конечное подсемейство Φ семейства Ω, покрывающее множество К, а следовательно, и F. Если множество F^c входит в Φ, то мы можем удалить его из Φ и получить открытое покрытие множества F. Таким образом, мы показали, что конечное подпокрытие покрытия {V_α} покрывает F.

Следствие.Если F замкнуто, а К компактно, то F∩К компактно.

Доказательство. Теоремы 2.26 (b) и 2.34 показывают, что множество F∩K замкнуто, а так как F∩K⊂K, то по теореме 2.35 множество F∩K компактно.

2.36. Если {К_α} - семейство компактных подмножеств метрического пространства X, такое, что пересечение любого конечного подсемейства семейства {К_α} непусто, то и 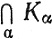непусто.

Доказательство. Зафиксируем множество K₁ из семейства {К_α} и положим G_α = K_α^c. Предположим, что в K₁ нет такой точки, которая принадлежала бы всем множествам К_α. Тогда множества G_α образуют открытое покрытие множества K₁; так как K₁ компактно, найдется конечный набор индексов α₁, ... , α_n, ... такой, что K₁⊂G_α1∩...∩G_αn. Но это означает, что множество

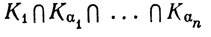
пусто. Мы получили противоречие с услсзиями теоремы.

Следствие.Если {К_n} - последовательность непустых компактных множеств, такая, что K_n⊃K_n+1 (n = 1, 2, 3...), то и множество 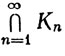непусто.

2.37. Теорема.Если Е - бесконечное подмножество компактного множества К, то Е имеет предельную точку, принадлежащую К.

Доказательство. Если бы никакая точка множества К не была предельной точкой множества Е, то каждая точка q∈К имела бы окрестность V_q, содержащую не более одной точки множества Е (а именно точку q, если q∈E). Ясно, что никакое конечное подсемейство семейства {V_q} не может покрыть множество Е;, то же верно и для К, так как Е⊂K. Но это противоречит компактности множества К.

2.38. Теорема.Если {I_n} - последовательность сегментов в R¹, такая, что I_n⊃I_n+1 (n = 1, 2, 3, ...), то множество 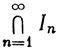непусто.

Доказательство. Если I_n = [a_n, b_n], то пусть E есть множество всех а_n. Тогда множество Е непусто и ограничено сверху (числом b₁). Пусть x - sup E. Если n и m - положительные целые числа, то

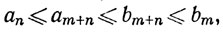
так что х≤b_m при каждом m. Поскольку очевидно, что а_m≤x, то мы видим, что х∈I_m при m = 1, 2, 3, ... .

2.39. Теорема.Пусть k - положительное целое число. Если {I_n} - последовательность k-мерных клеток, такая, что I_n⊃I_n+1 (n = 1, 2, 3, ...), то множество 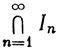непусто.

Доказательство. Пусть I_n состоит из всех точек х = (х₁, ..., x_k), таких, что

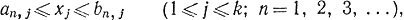
и пусть I_n,j = [a_n,j, b_n,j]. При каждом j последовательность {I_n,j} удовлетворяет предположениям теоремы 2.38. Значит, существуют вещественные числа x_j^* (1≤j≤k), такие, что

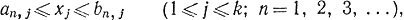
Полагая х^* = (х^*₁, ..., х^*_k), мы видим, что х^*∈I_n при n = 1, 2, 3,... . Теорема доказана.

2.40. Теорема.Любая k-мерная клетка компактна.

Доказательство. Пусть I есть k-мерная клетка, состоящая из всех точек x = (x₁,..., x_k), таких, что a_j≤j≤k. Положим

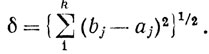
Тогда 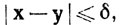если х∈I, у∈I.

Допустим, что вопреки утверждению теоремы существует открытое покрытие {G_α} множества I, не содержащее конечного подпокрытия множества I. Положим c_j = ^{(a_j + b_j)}/₂ Сегменты [a_j, c_j] и [c_j, b_j] определяют тогда 2^kk-мерных клеток Q_i, объединение которых есть I. Хотя бы одно из этих множеств Q_i (обозначим его I₁) не может быть покрыто никаким конечным подсемейством семейства {G_α} (в противном случае так была бы покрыта вся клетка I). Теперь мы разобьем I₁ и продолжим этот процесс. Мы получим последовательность {I_n}, обладающую следующими свойствами:

(a) I⊃I₁⊃I₂⊃I₃⊃...;

(b) I_n не покрывается никаким конечным подсемейством семейства {G_α};

(c) если х∈I_n и y∈I_n, то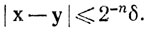

Из (а) и теоремы 2.39 следует, что существует точка х^*, принадлежащая всем множествам I_n. При некотором α имеем х^*∈G_α. Поскольку G_α открыто, существует r>0, такое, что из неравенства 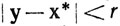следует включение у∈G_α. Если n столь велико, что 2^-nδ<r (такое n существует, ибо иначе 2ⁿ≤^δ/_r для всех положительных целых n, что невозможно), то из (с) следует, что I_n⊂G_α, а это противоречит утверждению (b).

Доказательство закончено.

Утверждение об эквивалентности свойств (а) и (b) в следующей теореме известно под названием теоремы Гейне - Бореля.

2.41. Теорема.Если множество Е из R^k обладает одним из трех следующих свойств, то оно обладает и двумя другими:

(с) каждое бесконечное подмножество множества Е имеет предельную точку, принадлежащую Е.

Доказательство. Если (а) выполнено, то Е⊂I, где I - некоторая k-мерная клетка, и (b) следует из теорем 2.40 и 2.35. Теорема 2.37 показывает, что (b) влечет за собой (с). Остается доказать, что из (с) следует (а).

Если множество Е не ограничено, то оно содержит точки х_n, такие, что

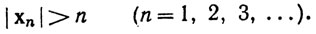
Множество S, состоящее из этих точек х_n, бесконечно и, очевидно, не имеет предельных точек в R^k и тем более в Е.

Таким образом, из (с) следует, что множество Е ограничено.

Если Е не замкнуто, то имеется точка x₀∈R^k, являющаяся предельной точкой множества Е, но не принадлежащая Е. При n = 1, 2, 3, ... имеются точки х_n∈E, такие, что 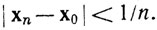. Пусть S - множество этих точек х_n. Тогда S - бесконечное множество (в противном случае 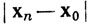имело бы постоянное положительное значение для бесконечного множества номеров n), х₀ - предельная точка множества S и в R^k нет других предельных точек множества S. Действительно, если y∈R^k, y ≠x₀, то

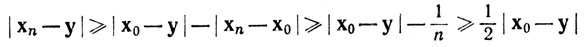
для всех n, за исключением некоторого конечного множества; это показывает, что у не является предельной точкой множества S (теорема 2.22).

Таким образом, S не имеет предельных точек в Е; значит, множество Е замкнуто, если выполнено (с).

Следует отметить в связи с этой теоремой, что (b) и (с) эквивалентны в любом метрическом пространстве (упражнение 13), но что из (а) в общем случае не следуют (b) и (с). Например, это так в пространстве 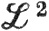, которое обсуждается в гл. 10. Один пример дается также в упражнении 9.

2.42. Теорема (Вейерштрасс).Всякое ограниченное бесконечное подмножество пространства R^k имеет предельную точку в R^k.

Доказательство. Будучи ограниченным, множество, о котором идет речь, содержится в некоторой k-мерной клетке I⊂R^k. По теореме 2.40 множество I компактно, поэтому, согласно теореме 2.37, множество Е имеет в I предельную точку.