
Метрические пространства
2.17. Определение. Говорят, что множество X, элементы которого мы будем называть точками, есть метрическое пространство, если любым двум точкам р и q множества X соответствует вещественное число d(p, q), называемое расстоянием от р до q, такое, что
(а) d(p, q)>0, если p≠q; d(p, р) = 0;
(b) d(p, q) = d(q, p);
(c) d(p, q)≤d(p, r) + d(r, q) при любом r∈Х.
2.18. Примеры. Самыми важными примерами метрических пространств с нашей точки зрения служат евклидовы пространства Rk, особенно R1 (вещественная прямая) и R2 (комплексная плоскость); расстояние в Rk определяется так:
(19)
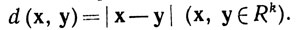
По теореме 1.64 метрика (19) удовлетворяет условиям определения 2.17.
Важно заметить, что каждое подмножество Y метрического пространства X в свою очередь является метрическим пространством с той же самой функцией расстояния. В самом деле, ясно, что если условия (а)-(с) определения 2.17 выполнены для р, q, r ∈Х, то они выполнены и для р, q, r, лежащих в Y.
Таким образом, каждое подмножество евклидова пространства - метрическое пространство. Другими примерами служат пространства 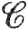 (K) и
(K) и 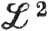 (μ), рассматриваемые соответственно в гл. 7 и 10.
(μ), рассматриваемые соответственно в гл. 7 и 10.
2.19. Определение.Под интервалом (а, и) мы будем понимать множество всех вещественных чисел х, таких, что а<х<b.
Под сегментом [а, b) мы будем понимать множество всех вещественных чисел х, таких, что а≤x≤b.
Иногда мы будем встречаться с полуинтервалами [а, b) и (а, b); первый состоит из всех х, таких, что а≤x<b, второй - из всех х, таких, что a<x≤b.
Если ai<bi при i = 1, ..., k, то множество всех точек х = (х1, ..., xk) в Rk, координаты которых удовлетворяют неравенствам ai≤xi≤bi (1≤i≤k), называется k-мерной клеткой. Таким образом, одномерная клетка - это сегмент, двумерная клетка - прямоугольник и т. д.
Если х∈Rk и r>0, то открытый (или замкнутый) шар В с центром в х радиусом r есть по определению множество всех у∈Rk таких, что 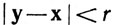
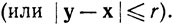
Назовем множество Е⊂Rkвыпуклым, если при любых х∈Е, у&38712;E и 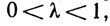
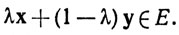
Например, шары выпуклы, ибо если 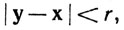
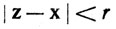 и
и 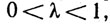 то
то
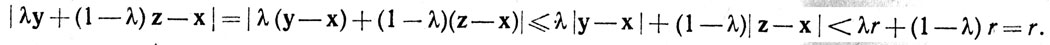
То же доказательство применимо и к замкнутым шарам. Легко видеть также, что k-мерные клетки выпуклы.
2.20. Определение. Пусть X - метрическое пространство. Все упоминаемые ниже точки и множества следует считать элементами и подмножествами пространства X.
(a) Окрестностью точки р называется множество Nr (р), состоящее из всех точек q, таких, что d(p, q)<r. Число r называется радиусом окрестности Nr (p).
(b) Точка р называется предельной точкой множества Е, если каждая окрестность точки р содержит точку q≠р, такую, что q∈E.
(c) Если р∈Е и р не является предельной точкой множества Е, то р называется изолированной точкой множества Е.
(d) Множество Е замкнуто, если каждая предельная точка множества Е является точкой множества Е.
(e) Точка р называется внутренней точкой множества Е, если она имеет окрестность N, такую, что N⊂Е.
(f) Множество Е открыто, если каждая точка множества Е является его внутренней точкой.
(g) Дополнением множества Е (обозначается символом Ес) называется множество всех точек р∈Х, таких, что р∉Е.
(h) Множество Е совершенно, если оно замкнуто и если каждая точка множества Е является его предельной точкой.
(i) Множество Е ограничено, если существуют вещественное число М и точка q∈X, такие, что d (p, q)<M при всех р∈Е.
(j) Множество Е всюду плотно в X, если каждая точка множества X является либо предельной точкой множества Е, либо принадлежит множеству Е (либо и то, и другое).
Отметим, что окрестностями в R1 служат интервалы, в то время как окрестности в R2 - это внутренности окружностей.
2.21. Теорема.Всякая окрестность является открытым множеством.
Доказательство. Рассмотрим окрестность E = Nr (p); пусть q - какая-нибудь точка множества Е. Тогда существует положительное вещественное число h, такое, что
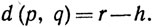
Для всех точек s, таких, что d(q, s)<h, мы имеем
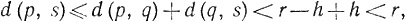
так что s∈E. Таким образом, q - внутренняя точка множества Е.
2.22. Теорема.Если р - предельная точка множества Е, то любая окрестность точки р содержит бесконечно много точек множества Е.
Доказательство. Предположим, что существует окрестность N точки р, содержащая только конечное число точек множества Е. Пусть q1, ..., qn - те точки множества N∩E, которые не совпадают с р. Положим
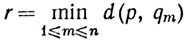
(так мы обозначаем наименьшее из чисел d(p, q1), ..., d(p, qn). Ясно, что минимум конечного множества положительных чисел - положительное число, так что r>0.
Окрестность Nr (p) не содержит ни одной точки q множества Е, такой, что q ≠ p, поэтому р не является предельной точкой множества Е. Это противоречие и доказывает теорему.
Следствие.Конечное множество точек не имеет предельных точек.
2.23. Примеры. Рассмотрим следующие подмножества пространства R2:
(а) множество всех комплексных z, таких, что 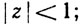
(b) множество всех комплексных z, таких, что 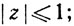
(c) некоторое конечное множество;
(d) множество всех целых чисел;
(e) множество, состоящее из чисел 1/n (n = 1,2, 3, ...).
Отметим, что последнее множество Е имеет предельную точку (а именно z = 0), но никакая точка множества Е не является его предельной точкой. Мы хотим подчеркнуть разницу между свойствами множества иметь предельную точку и содержать предельную точку.
(f) Множество всех комплексных чисел (т. е. R2);
(g) интервал (а, b).
Отметим, что множества (d), (e), (g) можно рассматривать и как подмножества пространства R1.
Некоторые свойства этих множеств перечислены в следующей таблице:

В строке (g) мы не заполнили второй клетки. Причина этого в том, что интервал (а, b) не есть открытое множество, если рассматривать его как подмножество пространства R2, но он является открытым подмножеством пространства R1.
2.24. Теорема.Пусть {Еα} - (конечное или бесконечное) семейство множеств Еα. Тогда
(20)
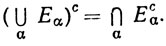
Доказательство. Пусть А и B - множества, стоящие соответственно слева и справа в равенстве (20). Если х∈А, то 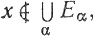 значит, х&38713;Еα при всех α, поэтому хẄЕсα при всех α, так что х∈∩Ecα. Таким образом, A⊂B.
значит, х&38713;Еα при всех α, поэтому хẄЕсα при всех α, так что х∈∩Ecα. Таким образом, A⊂B.
Обратно, если х∈В, то х∈Ecα при всех α, значит, х∉Еα при всех α, поэтому 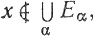 так что x∈
так что x∈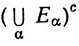 . Таким образом, В⊂А.
. Таким образом, В⊂А.
Следовательно, А = В.
2.25. Теорема.Множество Е открыто тогда и только тогда, когда его дополнение замкнуто.
Доказательство. Сначала предположим, что Ес замкнуто. Выберем х∈Е. Тогда х∉Ес и х не является предельной точкой множества Ес. Значит, существует окрестность N точки х, такая, что множество Ec∩N пусто, т. е. N⊂E. Таким образом, х - внутренняя точка множества Е, и Е открыто.
Теперь предположим, что Е открыто. Пусть х - предельная точка множества Ес. Тогда каждая окрестность точки х содержит некоторую точку множества Ес, так что х не является внутренней точкой множества Е. Поскольку Е открыто, это значит, что х∈Ес. Следовательно, Ес замкнуто.
Следствие.Множество F замкнуто тогда и только тогда, когда его дополнение открыто.
2.26. Теорема, (а) Для любого семейства {Gα} открытых множеств множество 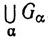 открыто.
открыто.
(b) Для любого семейства 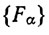 замкнутых множеств множество
замкнутых множеств множество 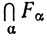 замкнуто.
замкнуто.
(c) Для любого конечного семейства G1, ..., Gn открытых множеств множество 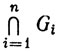 открыто.
открыто.
(d) Для любого конечного семейства F1, ..., Fn замкнутых множеств множество 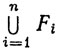 замкнуто.
замкнуто.
Доказательство. Положим 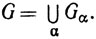 Если х∈G, то х∈Gα при некотором α. Так как х - внутренняя точка множества Gα то х - внутренняя точка множества G, и G открыто. Утверждение (а) доказано.
Если х∈G, то х∈Gα при некотором α. Так как х - внутренняя точка множества Gα то х - внутренняя точка множества G, и G открыто. Утверждение (а) доказано.
По теореме 2.24 имеем
(21)
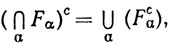
а по теореме 2.25 множества Fcα открыты. Значит, из (а) следует, что множество (21) открыто, так что множество 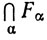 замкнуто.
замкнуто.
Теперь положим 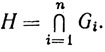 Для любого x∈H существует окрестность Ni точки х радиуса r такая, что
Для любого x∈H существует окрестность Ni точки х радиуса r такая, что 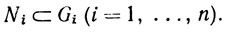 Положим
Положим
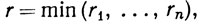
и пусть N - окрестность точки х радиуса r. Тогда N⊂Gi при i = 1, ..., n, так что N⊂Н, и множество Н открыто. Переходя к дополнениям, мы выведем (d) из (с):
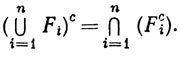
2.27. Пример. В утверждениях (с) и (d) предыдущей теоремы конечность семейств существенна. Действительно, пусть Gn - интервал 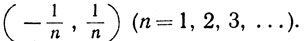 Тогда Gn - открытое подмножество прямой R1. Положим
Тогда Gn - открытое подмножество прямой R1. Положим 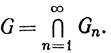 Тогда G состоит из единственной точки (а именно, x = 0) и поэтому не является открытым подмножеством из R1.
Тогда G состоит из единственной точки (а именно, x = 0) и поэтому не является открытым подмножеством из R1.
Таким образом, пересечение бесконечного семейства открытых множеств не обязано быть открытым. Подобным образом, объединение бесконечного семейства замкнутых множеств не обязано быть замкнутым.
2.28. Теорема.Пусть Е - замкнутое множество вещественных чисел, ограниченное сверху. Пусть y = sup E. Тогда у∈Е.
Сравните это утверждение с примерами 1.35.
Доказательство. Допустим, что у∉Е. Для каждого h>0 существует точка х∈Е, такая, что у - h≤x≤y, так как иначе у - h было бы верхней границей множества Е. Таким образом, каждая окрестность точки у содержит некоторую точку х множества Е, причем х≠у, так как у∉Е. Следовательно, у - предельная точка множества Е, не принадлежащая Е, так что множество Е не замкнуто. Но это противоречит условию теоремы.
2.29. Замечание. Допустим, что Е⊂Y⊂X, где X - метрическое пространство. То, что Е - открытое подмножество пространства X, означает, что с каждой точкой р∈Е связано положительное число r, для которого из условий d(p, q)<r, q∈X следует включение q∈. Но мы уже заметили (п. 2.18), что Y - тоже метрическое пространство, так что наше определение с таким же успехом можно отнести к Y. Для полной точности мы будем говорить, что множество Е открыто относительно Y, если каждой точке р∈Е отвечает число r>0, такое, что q∈E, если d(p,q)<r и q∈Y. Пример 2.23 (g) показывает, что множество может быть открытым относительно Y, не будучи открытым подмножеством пространства X. Однако между этими понятиями имеется простое соотношение, которое мы сейчас установим.
2.30. Теорема.Пусть Y⊂X. Подмножество Е множества Y открыто относительно Y тогда и только тогда, когда E = Y∩G для некоторого открытого подмножества G пространства X.
Доказательство. Допустим, что Е открыто относительно Y. Для каждого р∈Е найдется положительное число rр, такое, что из условий d(p, q)<rp, q∈Y следует, что q∈E. Пусть Vp - множество всех q∈X, таких, что d(p, q)<rp; положим
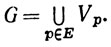
Тогда по теоремам 2.21 и 2.26 G - открытое подмножество пространства X.
Поскольку р∈Vp при всех р∈Е, ясно, что Е⊂G∩Y. Согласно нашему выбору окрестности Vp, имеем Vp∩Y⊂Е при каждом р∈Е, так что G⊍Y⊂E. Таким образом, E = G⊍Y, и половина теоремы доказана.
Обратно, если множество G открыто в X и E = G⊍Y, то каждая точка р∈Е имеет окрестность Vp⊂G. Тогда Vp⊍Y⊂E, так что множество Е открыто относительно Y.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'