Глава 2. Элементы теории множеств

Конечные, счетные и несчетные множества

Мы начнем этот раздел с определения понятия функции.

2.1. Определение. Рассмотрим два множества А и В, элементами которых могут быть любые объекты, и предположим, что каждому элементу х множества A некоторым способом поставлен в соответствие элемент множества В, который мы обозначим через f(х). Тогда f называется функцией из A в В (или отображением множества А в В).

Множество А называется областью определения функции f (мы будем говорить также, что f определена на A), а элементы f(х) называются значениями f. Множество всех значений функции f называется ее областью значений.

2.2. Определение. Мы будем говорить, что множество А есть подмножество множества В, и писать A⊂В (или В⊃A), если каждый элемент множества А является элементом множества В. Если, кроме того, в В имеется элемент, не принадлежащий А, то А называется собственным подмножеством множества В.

В частности, пустое множество ∅ служит подмножеством любого множества, и A⊂ A, каково бы ни было множество A.

Если А ⊂ В и В ⊂ A, то мы будем писать А = В.

2.3. Замечание. То обстоятельство, что пустое множество является подмножеством любого множества, связано с одной логической тонкостью, часто вызывающей трудности у начинающих.

Из определения 2.2 ясно, что если множество A не есть подмножество множества В, то должно быть верным следующее утверждение: "существует элемент х, такой, что х ∈А и х ∉В". Но если A пусто, то не существует такого х, что х ∈А, и высказанное только что утверждение ложно.

Подобные рассуждения применимы всегда, когда мы хотим проверить, что пустое множество удовлетворяет некоторым условиям.

2.4. Определение. Пусть A и В - два множества, и пусть f - отображение А в В. Если Е ⊂;А, то f(E) определяется как множество всех элементов f(x) для х ∈Е. Мы будем называть f(E) образом множества Е при отображении f. В этих обозначениях f(A) - это множество значений f. Ясно, что f(A)⊂B;. Если f(A) = B, то мы будем говорить, что f отображает А на В. (Заметим, что в соответствии с этим словоупотреблением на означает большее, чем в.)

Если Е⊂В, то f^-1 (E) обозначает множество всех х∈А, таких, что f(х)∈Е. Мы будем называть f^-1(Е) прообразом множества Е при отображении f. Если у ∈В, то f^-1(у) - это множество всех х ∈А, таких, что f(x) = y. Если при каждом у ∈В множество f^-1(y) состоит не более чем из одного элемента A, то f называется взаимно однозначным отображением А в В. Это можно выразить следующим образом: отображение f множества A в В взаимно однозначно, если f(x₁)≠f(x₂) каждый раз, когда x₁≠x₂, x₁ ∈A, x₂ ∈A.

(Запись x₁≠x₂ означает, что x₁ и x₂ - различные элементы; в противном случае мы пишем x₁ = x₂.)

2.5. Определение. Если существует взаимно однозначное отображение множества A на множество В, то мы будем говорить, что между A и В может быть установлено взаимно однозначное соответствие, или что A и В имеют одно и то же кардинальное число, или, короче, что A и В эквивалентны, и будем писать А~В. Это отношение, очевидно, обладает следующими свойствами:

рефлексивность: А~А;

симметричность: если А~В, то В~А;

транзитивность: если A~B и В~С, то А~С.

Всякое отношение, обладающее этими тремя свойствами, называется отношением эквивалентности.

2.6. Определение. Пусть n - любое положительное целое число; J_n - множество, элементами которого служат целые числа 1, ..., n; J - множество, состоящее из всех положительных целых чисел; A - любое множество. Мы будем говорить, что

(a) А конечно, если A~J_n при некотором n (пустое множество также считается конечным);

(b) А бесконечно, если A не является конечным;

(c) А счетно, если А~J;

(d) А несчетно, если A не конечно и не счетно;

(e) А не более чем счетно, если A или конечно, или счетно.

Если A и В - конечные множества, то очевидно, что А~В тогда и только тогда, когда A и В содержат одно и то же число элементов. Однако для бесконечных множеств смысл слов "содержат одно и то же число элементов" становится очень туманным.

Он проясняется с помощью понятия взаимно однозначного соответствия.

2.7. Пример. Пусть A - множество всех целых чисел. Тогда A - счетное множество. Действительно, рассмотрим следующее расположение множеств А и J

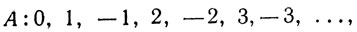
В этом примере мы можем даже указать в явном виде формулу для отображения f множества J в A, устанавливающего взаимно однозначное соответствие между этими множествами:

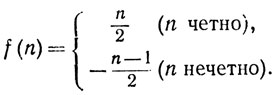
2.8. Замечание. Конечное множество не может быть эквивалентно своему собственному подмножеству. Однако для бесконечных множеств это возможно, как показывает пример 2.7, в котором J - собственное подмножество множества A.

В действительности мы могли бы заменить определение 2.6 (b) следующей формулировкой: A бесконечно, если A эквивалентно одному из своих собственных подмножеств.

2.9. Определение.Последовательностью мы будем называть функцию f, определенную на множестве J всех положительных целых чисел. Если f(n) = х_n при n∈J, то принято обозначать последовательность / символом {хп} или писать х₁, х₂, х₃, .... Значения функции f, т. е. элементы х_n, называются членами последовательности. Если A - некоторое множество и если х_n∈А при всех n∈J, то {х_n} называется последовательностью в A, или последовательностью элементов множества А.

Заметим, что члены х₁, х₂, х₃, ... последовательности не обязаны быть различными.

Ввиду того что всякое счетное множество служит множеством значений некоторой взаимно однозначной функции, определенной на J, мы можем рассматривать всякое счетное множество как множество значений некоторой последовательности с различными членами. Допуская некоторую вольность речи, говорят, что элементы любого счетного множества можно "расположить в последовательность".

Иногда удобно заменить в этом определении J множеством всех неотрицательных целых чисел, т. е. начинать с 0, а не с 1.

2.10. Теорема.Всякое бесконечное подмножество счетного множества А счетно.

Доказательство. Предположим, что Е⊂A и E бесконечно. Расположим элементы х множества А в последовательность {х_n} с различными членами. Построим последовательность {n_k} следующим образом.

Пусть n₁ - наименьшее целое положительное число, такое, что х_n1∈Е. Если n₁,..., n_k-1 (k = 2, 3, 4, ...) уже выбраны, то пусть n_k - наименьшее целое число, большее n_k-1 и такое, что х_nk∈Е.

Полагая f(k) = x_nk (k = 1, 2, 3, ...), мы получим взаимно однозначное соответствие между E и J.

Эта теорема показывает, что, грубо говоря, счетные множества представляют "наименьшую" бесконечность: никакое несчетное множество не может быть подмножеством счетного.

2.11. Определение. Пусть А и Ω - множества; предположим, что каждому элементу α множества A сопоставлено некоторое подмножество множества Ω, которое мы обозначим через Е_α.

Множество, элементами которого служат множества Е_α, будет обозначаться через {E_α}. Вместо того чтобы говорить о множестве множеств, мы иногда будем говорить о наборе множеств или о семействе множеств^*.

^* (На самом деле "множество множеств" - это понятие, по существу отличное от понятия "семейств множеств", которое здесь определено. Семейство множеств есть отображение множества А в множество всех подмножеств множества Ω. Может оказаться, что Е_α' = Е_α" при α'≠α", α', α" ∈Ω.- Прим. перев.)

Объединение семейства множеств {Е_α} определяется как множество S, такое, что х*#8712;S тогда и только тогда, когда х∈Е_α хотя бы при одном α∈A. Мы будем пользоваться обозначением

(1)

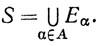
Если A состоит из целых чисел 1, ..., n, то обычно пишут

(2)

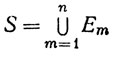
или

(3)

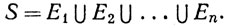
Если A - множество всех положительных целых чисел, то обычное обозначение таково:

(4)

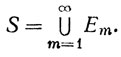
Символ ∞ в (4) указывает только, что берется объединение счетного семейства множеств. Его не следует смешивать с символами +∞, -∞, введенными в определении 1.39.

Пересечение семейства множеств {Е_α} определяется как множество Р, такое, что х∈Р тогда и только тогда, когда х&38712;Е_α при всех α∈А. Мы будем пользоваться обозначением

(5)

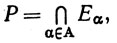
или

(6)

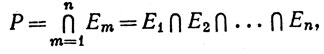
или

(7)

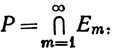
как для объединений. Если множество А∩В не пусто, то мы будем говорить, что А и В пересекаются, в противном случае - что они не пересекаются.

2.12. Примеры, (а) Допустим, что E₁ состоит из чисел 1, 2, 3, а E₂ - из чисел 2, 3, 4. Тогда E₁∪E₂ состоит из чисел 1, 2, 3,4, в то время как E₁∩E₂ - из чисел 2, 3.

(b) Пусть А - множество всех вещественных чисел х, таких, что 0<x<1. Для любого х∈А пусть Е_х - множество всех вещественных чисел _у, таких, что 0<y<х. Тогда

(i) E_x ⊂E_z тогда и только тогда, когда 0<x≤z<1;

(ii)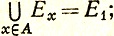

(iii) 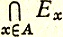пусто.

Утверждения (i) и (ii) очевидны. Чтобы доказать (iii), заметим, что при любом у&$62;0 имеем у∉Е_х, если х<у. Значит,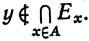

2.13. Замечания. Многие свойства объединений и пересечений совершенно аналогичны свойствам сумм и произведений. В действительности слова "сумма" и "произведение" иногда употребляют в этом смысле и вместо ∪ и ∩ пишут ∑ и ∏.

Законы коммутативности и ассоциативности тривиально выполняются

(8)

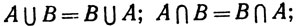
(9)

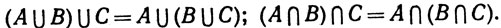
Этим оправдано отсутствие скобок в (3) и (6). Закон дистрибутивности также выполняется:

(10)

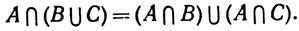
Чтобы доказать это, обозначим левую и правую части равенства (10) соответственно через Е и F.

Допустим, что х∈Е. Тогда х∈А и х∈В∪С, т. е. х∈В или х∈С (или и то и другое). Значит, х∈А∩В или х∈А∩С, так что x∈F. Таким образом, E⊂F.

Предположим теперь, что x∈F. Тогда х∈А∩В или х∈А∩С. Таким образом, х∈А и х∈В∪С. Значит, x∈A∩(B∪C), так что F⊂E. Следовательно, E = F.

Перечислим еще несколько легко проверяемых соотношений:

(11)

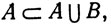
(12)

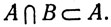
Если ∅ обозначает пустое множество, то

(13)

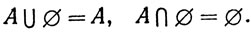
Если А⊂В, то

(14)

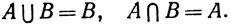
2.14. Теорема.Пусть {Е_n}, n = 1, 2, 3, ..., - последовательность счетных множеств; положим

(15)

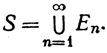
Тогда множество S счетно.

Доказательство. Расположим каждое множество Е_n в последовательность {x_nk}, k = 1, 2, 3, ..., и рассмотрим бесконечную таблицу

(16)

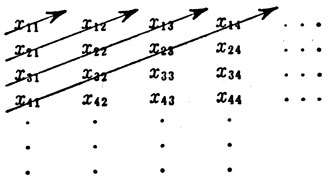
в которой элементы множества Е_n образуют n-ю строку. Эта таблица содержит все элементы множества S. Эти элементы можно расположить в последовательность так, как указывают стрелки:

(17)

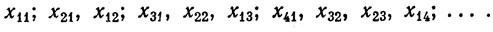
Если какие-нибудь два множества Е_n имеют общие элементы, то они появятся в (17) более чем один раз. Значит, существует подмножество Т множества всех положительных целых чисел, такое, что S˜Т, откуда следует, что множество 5 не более чем счетно (теорема 2.10). Поскольку E₁⊂S и E₁ бесконечно, то и S бесконечно, и поэтому счетно.

Следствие.Допустим, что А не более чем счетно и что при каждом α∈А множество В_α не более чем счетно. Положим

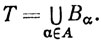
Тогда множество Т не более чем счетно.

Действительно, Т эквивалентно некоторому подмножеству множества (15).

2.15. Теорема.Пусть А - счетное множество, и пусть В_n - множество всех наборов (а₁, ...,а_n) из n членов, где а_k∈A (k = 1, ..., n) и элементы а₁, ..., а_n не обязательно различны. Тогда множество В_n счетно.

Доказательство. То, что множество В₁ счетно,- очевидно. Допустим, что множество В_n-1 счетно (n = 2, 3, 4, ...). Элементы В_n имеют вид

(18)

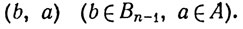
При каждом фиксированном b множество всех пар (b, а) эквивалентно множеству А и, значит, счетно. Таким образом, В_n - объединение счетного множества счетных множеств. По теореме 2.14 В_n счетно.

Утверждение теоремы доказано по индукции.

Следствие.Множество всех рациональных чисел счетно.

Доказательство. Применим теорему 2.15, взяв n = 2 и заметив, что каждое рациональное число r имеет вид ^b/_a, где а и b - целые числа. Множество пар (а, b), а поэтому и множество дробей ^b/_a, счетно.

На самом деле даже множество всех алгебраических чисел счетно (см. упражнение 5).

Следующая теорема показывает, однако, что не все бесконечные множества счетны.

2.16. Теорема.Пусть А - множество всех последовательностей, элементы которых - цифры 0 и 1. Множество А несчетно.

Элементами А служат последовательности вида 1, 0, 0, 1, 0, 1, 1, 1,....

Доказательство. Пусть Е - счетное подмножество множества А, и пусть Е состоит из последовательностей s₁, s₂, s₃, ... . Построим последовательность s следующим образом. Если n-я цифра в s_n равна 1 (соответственно 0), то пусть n-я цифра в s равна 0 (соответственно 1). Тогда последовательность s отличается от каждого элемента множества Е хотя бы одним членом, значит, s∉E. Но очевидно, что s∈A, так что Е - собственное подмножество множества А.

Мы показали, что каждое счетное подмножество множества А является собственным подмножеством. Следовательно, А несчетно (потому что в противном случае А было бы своим собственным подмножеством, что невозможно).

Идею приведенного доказательства впервые высказал Кантор. Такой метод доказательства называют канторовским диагональным процессом, потому что если последовательности s₁, s₂, ... расположить в виде таблицы типа (16), то при построении новой последовательности будут учитываться элементы диагонали.

Читатели, знакомые с двоичным представлением вещественных чисел, когда за основание вместо числа 10 берется число 2, заметят, что из теоремы 2.16 следует, что множество всех вещественных чисел несчетно. Второе доказательство этого факта мы дадим в теореме 2.43.