Упражнения

1. Пусть r - рациональное число (r≠0), a x - иррациональное. Доказать, что числа r + x и rх иррациональны.

2. Доказать, что между любыми двумя вещественными числами содержится иррациональное число.

3. Доказать, что не существует рационального числа, квадрат которого равен 12.

4. Пусть x>0, y>0 и n - положительное целое число. Доказать, что

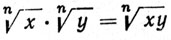
(ср. с теоремой 1.37).

5. Если х<0, а r - рациональное число (r = ⁿ/_m), то положим

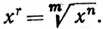
Доказать, что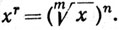

6. Доказать, что если x>1, то x^p<x^q при любых рациональных р, q, таких, что p<q.

7. Определить x^y для х>1 и вещественного у, используя упражнение 6 и метод теоремы 1.37, и доказать, что

(a) x^y<x^z, если 1<x, y<z;

(b) x^y<z^y, если 1<x<z, y&362;0;

(c) x^y+z = x^yx^z.

8. Как нужно изменить упражнения 6 и 7, если 0≤x≤1?

9. Пусть b&362;1, х&362;0. Доказать, что существует одно и только одно вещественное число у, такое, что x = b^y. Это число у называется логарифмом х при основании b.

10. В каких пунктах нашего изложения теории вещественных чисел возникли бы трудности, если бы было опущено условие III определения 1.4?

11. Если z₁, ..., z_n - комплексные числа, то

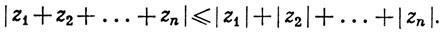
12. Если х и у - комплексные числа, то

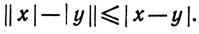
13. Теорема 1.36 была выведена из теоремы 1.32. На самом деле эти теоремы равносильны. Чтобы убедиться в этом, докажите теорему 1.32, не пользуясь сечениями в множестве рациональных чисел, а используя как постулат теорему 1.36 и обычные арифметические свойства вещественных чисел.

14. Пусть z - такое комплексное число, что 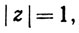т. е. z 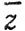= 1. Вычислить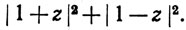

15. При каких условиях в неравенстве Шварца имеет место равенство?

16. Предположим, что k≥3, x, y∈R^k, 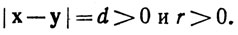Доказать, что

(a) если 2r>d, то существует бесконечное множество точек z∈R^k, таких, что

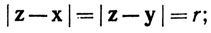
(b) если 2r = d, то существует в точности одна такая точка z;

(c) если 2r<d, то не существует таких z.

Как нужно изменить эти утверждения, если k = 2, k = 1?

17. Доказать, что

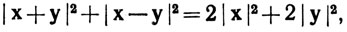
если x∈R^k, y∈R^k. Истолковать это геометрически, как некоторое утверждение о параллелограммах.

18. Доказать, что если k≥2 и х∈R^k, то существует вектор y∈R^k такой, что у≠0, но х - у = 0. Верно ли это при k = 1?

19. Пусть а∈R^k, b∈R^k. Найти c∈R^k и r>0, такие, что |x -a| = 2|х - b| тогда и только тогда, когда |х -с| = r.

(Решение: 3с = 4b - а, 3r = 2|b - а|.)