Евклидовы пространства

1.63. Определения. Для каждого положительного целого k обозначим через R^k множество всех упорядоченных последовательностей из k вещественных чисел

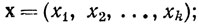
числа x₁, ...,x_k называются координатами элемента х. Элементы множества R^k называются точками, или векторами, особенно при k>1. Мы будем обозначать векторы буквами, набранными жирным шрифтом. Если y = (y₁,...,y_k) и α - вещественное число, то положим

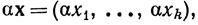
так что x + y ∈R^k и αx∈R^k. Тем самым определено сложение векторов, а также умножение вектора на вещественное число (скаляр). Эти две операции подчиняются законам коммутативности, ассоциативности и дистрибутивности (доказательство тривиально, так как аналогичным законам подчиняются вещественные числа) и превращают R^kв векторное пространство над полем вещественных чисел. Нулевой элемент пространства R^k (иногда называемый началом, или нулевым вектором) - это точка 0, все координаты которой равны 0.

Мы определим еще так называемое скалярное (или внутреннее) произведение векторов х и у:

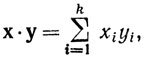
а также норму вектора х:

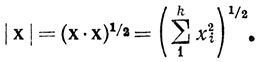
Определенная таким образом структура (векторное пространство R^k со скалярным произведением и нормой) называется евклидовым k-мерным пространством.

1.64. Теорема.Пусть х, у, z∈R^k и α-вещественное число. Тогда

(a)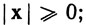

(b) 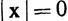тогда и только тогда, когда х = 0;

(c)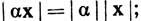

(d)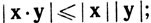

(e)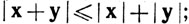

(f)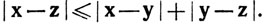

Доказательство. Утверждения (а), (b) и (с) очевидны, a (d) следует непосредственно из неравенства Шварца. В силу (d), имеем

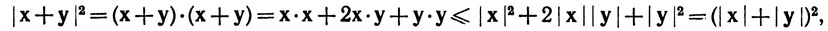
что доказывает (е). Наконец, (f) следует из (е), если заменить х на х - у, у на у - z.

1.65. Замечания. Теорема 1.64 (а), (b) и (f) позволит нам (см. гл. 2) рассматривать R^k как метрическое пространство.

Пространство R¹ (множество всех вещественных чисел) обычно называют прямой, или вещественной прямой. Аналогичным образом, R² называют плоскостью (ср. определения 1.41 и 1.63). В этих двух случаях норма - это абсолютная величина соответствующего вещественного или комплексного числа.