Комплексные числа

1.41. Определение.Комплексным числом называется пара вещественных чисел а, b (в таком порядке). Обозначим это комплексное число через (а, b).

В этом разделе буквами х, у, z будут обозначаться комплексные числа, буквами а, b, с, ...- вещественные числа; мы будем (временно) писать

1.42. Определение. Пусть х = (а, b), у = (с, d). Тогда х = у тогда и только тогда, когда а = с и b = d. Паре х, у сопоставим два комплексных числа, обозначаемых через х + у, ху и определенных следующим образом:

1.43. Теорема.Для операций сложения и умножения, введенных в определении 1.42, выполняются законы коммутативности, ассоциативности и дистрибутивности.

Доказательство. Пусть х = (а, b), у = (с, d), z = (e, f).

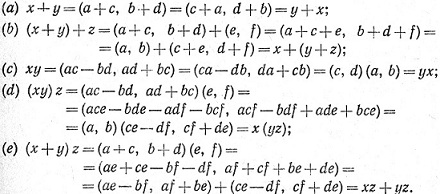
1.44. Теорема.Для любого комплексного х имеем х + n = х, хn = n, хu = х.

Доказательство. Это следует непосредственно из определения 1.42.

1.45. Теорема.Если x + y = x + z, то y = z.

Доказательство. Если у≠z, то, как показывают определение 1.42 и теорема 1.18, х + y ≠ x + z.

1.46. Теорема.Для любого комплексного числа х существует одно и только одно комплексное число у, такое, что x + y = n.

Мы обозначим это число у через -х.

Доказательство. Единственность следует из теоремы 1.45. Чтобы доказать существование, допустим, что х = (а, b), и положим -х = (-a, -b).

1.47. Теорема.Если писать х - у вместо х + (-у), то

так что не возникнет никакой неясности, если мы будем все эти выражения записывать в виде -ху.

Доказательства тривиальны.

1.48. Определение. Пусть х = (а, b). Мы будем называть абсолютной величиной числа х число 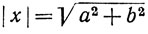(мы рассматриваем только неотрицательное значение квадратного корня, которое определяется единственным образом по теореме 1.37).

Заметим, что абсолютная величина комплексного числа - неотрицательное вещественное число.

1.49. Теорема. Для любых комплексных чисел х, у имеем

(а) 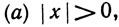если х≠n, и |n| = 0;

(b)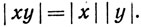

Доказательство. Свойство (а) тривиально. Что касается (b), то пусть х = (а, b), у = (с, d). Тогда 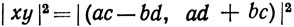= a²c² + b²d² + a²d² + b²c² = (a² + b²)(c² + d²) = 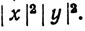Значит,

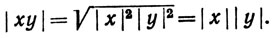
Доказать последнее равенство мы предоставляем читателю (упражнение 4).

1.50. Теорема. Если хy = n, то либо х = n, либо у = n.

Доказательство. Если ху = n, то по теореме 1.49

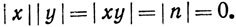
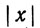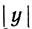Поскольку и вещественны, отсюда следует, что л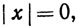ибо либо 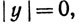т. е. либо х = n, либо у = n.

1.51. Теорема. Если х≠n и xy = xz, то y = z.

Доказательство. Имеем

По теореме 1.50 y - z = n, т. е. y = z.

1.52. Теорема. Для любого комплексного х≠n существует одно и только одно комплексное число у (которое мы будем записывать в виде ^и/_х), такое, что ху = u.

Доказательство. Единственность следует из теоремы 1.51.

Пусть х = (а, b). Положим

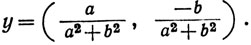
Тогда

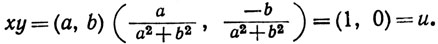
1.53. Теорема.Если х≠n, то для любого комплексного у существует одно и только одно комплексное z (которое мы будем записывать в виде ^у/_х), такое, что xz = y.

Доказательство. Положим z = (^u/_x)*y. Тогда

Итак, мы показали, что комплексные числа со сложением и умножением, введенными в определении 1.42, подчиняются всем обычным законам арифметики.

1.54. Теорема. Для любых вещественных чисел а и b имеем

(a) (а, 0) + (b, 0) = (а + b, 0),

(b) (а, 0)(b, 0) = (ab, 0),

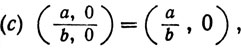
если b≠0,

(d)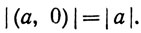

В (d) символ 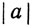нужно понимать в смысле определения 1.24.

Доказательство тривиально.

Теорема 1.54 показывает, что комплексные числа вида (а, 0) обладают теми же арифметическими свойствами, что и вещественные числа а.

Мы можем поэтому отождествить (а, 0) с а; это отождествление превращает множество всех вещественных чисел в подмножество системы комплексных чисел.

В частности, мы будем теперь писать 0 вместо n и 1 вместо u.

Читатель, вероятно, заметил, что мы построили арифметику комплексных чисел, не вводя таинственного обозначение 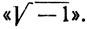Теперь мы хотим показать, что обозначение (а, b) равносильно более привычному a + bi.

1.55. Определение. i = (0, 1).

1.56. Теорема.i² = - 1.

Доказательство. i² = (0, 1)(0, 1) = (- 1, 0) = -1.

1.57. Теорема.Если а и b - вещественные числа, то (а, b) = а + bi.

Доказательство. а + bi = (а, 0) +(b, 0)(0, 1) = (а, 0) + (0, b) = (a, b).

1.58. Теорема.Если х и у - комплексные числа, то

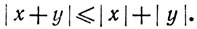
Доказательство. Если х + y = 0, то доказывать нечего. Допустим, что х + у ≠0, и положим

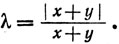
Умножая на х + у, мы заключаем по теореме 1.49(b), что |h| = 1. Кроме того, λх + λу - вещественное число. Если λх = (а, b) и λу = (с, d), то, как показывает определение 1.48,

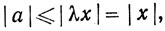
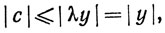
значит,

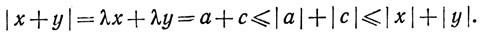
1.59. Определение. Если а и b - вещественные числа и z = a + bi, то комплексное число 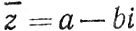называется сопряженным с z.

1.60. Теорема. Если х, у - комплексные числа, то

(a)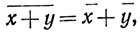

(b)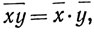

(c) 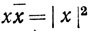(значит, число x 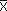вещественно и неотрицательно),

(d) х + 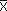- вещественное число,

(e) если х вещественно, то 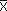= х.

Доказательства этих утверждений тривиальны.

1.61. Обозначение. Если х₁,..., x_n - комплексные числа, то мы будем писать

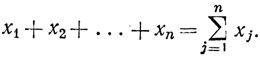
Мы закончим этот раздел важным неравенством, известным под названием неравенства Шварца.

1.62. Теорема.Если а₁,...,а_n и b₁,...,b_n - комплексные числа, то

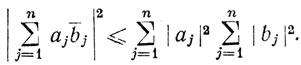
Доказательство. Положим 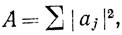, , 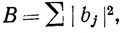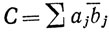во всех суммах в доказательстве j пробегает множество чисел 1,...,n). Если B = 0, то b₁ = ... = b_n = 0, и заключение тривиально. Допустим поэтому, что B>0. По теореме 1.60 имеем

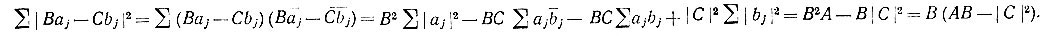
Мы видим, что

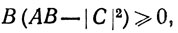
так как все слагаемые в первой сумме неотрицательны. Отсюда следует, что 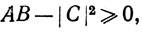поскольку B>0. Но это и есть требуемое неравенство.