Расширенная система вещественных чисел

1.39. Определение. Расширенная система вещественных чисел состоит из системы вещественных чисел, к которой присоединены два символа -∞ и +∞, причем выполняются следующие свойства:

(а) если х - вещественное число, то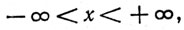

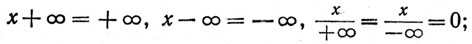
(б) если х>0, то

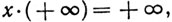
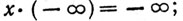
(с) если x<0, то

Если необходимо подчеркнуть различие между символами -∞, +∞, с одной стороны, и вещественными числами, с другой, то последние называют конечными^*.

^* (Такой способ расширения множества всех вещественных чисел не согласуется с теорией сечений, при помощи которой только что пополнялось множество всех рациональных чисел. Действительно, центральное место в теории Дедекинда занимает доказательство существования множества (иррациональных чисел), элементы которого связаны друг с другом и с рациональными числами многочисленными соотношениями (а не просто введение новых символов, удовлетворяющих определенным аксиомам). С этой точки зрения расширение множества всех вещественных чисел можно было бы "построить", рассмотрев еще два сечения: для первого из них (обозначаемого -∞) нижним классом служит пустое множество, а для второго (обозначаемого +∞) - множество всех рациональных чисел. Разумно определив смысл символов x±∞, x*±∞, отношений <, > и т. д., можно было бы доказать свойства (а), (b), (с).- Прим. перев.)

1.40. Определение. Пусть Е- множество, элементы которого принадлежат расширенной системе вещественных чисел. Если Е не ограничено сверху (т. е. если для любого вещественного у существует элемент х∈Е, такой, что y<x), то верхняя грань множества Е по определению равна +∞.

Аналогичным образом нижняя грань множества Е, не ограниченного снизу, по определению равна -∞.

Итак, в расширенной системе вещественных чисел каждое множество имеет inf и sup. Это и есть главная причина введения символов -∞ и +∞.