Вещественные числа

Подведем итоги сказанному в предыдущем разделе. Мы рассмотрели некоторые множества рациональных чисел, которые мы назвали сечениями. Были определены отношение порядка и две операции, названные сложением и умножением, и мы доказали, что получившаяся арифметика сечений подчиняется тем же законам, что и арифметика рациональных чисел. Иными словами, множество всех сечений было превращено в упорядоченное поле.

Особое внимание было уделено специальному классу сечений, так называемым "рациональным сечениям", и мы обнаружили, что при замене рациональных чисел r соответствующими сечениями r* суммы, произведения и порядок сохраняются (теорема 1.28). Этот же факт можно выразить, сказав, что упорядоченное поле всех рациональных чисел изоморфно упорядоченному полю всех рациональных сечений; это позволяет нам отождествить рациональное сечение r* с рациональным числом r. Разумеется, r* - это не то же самое, что r, но свойства, с которыми мы имеем дело (арифметика и порядок), одинаковы в этих двух полях.

Теперь определим, что мы будем понимать под вещественным числом.

1.31. Определение. В дальнейшем сечения будут называться вещественными числами. Рациональные сечения будут отождествляться с рациональными числами (и будут называться рациональными числами). Все другие сечения будут называться иррациональными числами.

Таким образом, множество всех рациональных чисел оказывается подмножеством системы вещественных чисел. Теорема 1.29 показывает, что между любыми двумя вещественными числами имеется рациональное число, а теорема 1.30 показывает, что каждое вещественное число а есть множество всех рациональных чисел р, таких, что р<α.

В следующей теореме высказано чрезвычайно важное свойство системы вещественных чисел.

1.32. Теорема (Дедекинд).Пусть А и В - такие множества вещественных чисел, что

(d) если α∈ А и β∈ В, то α<β.

Тогда существует одно (и только одно) вещественное число γ, такое, что α≤γ при всех α∈A и γ≤β при всех β∈ B.

Прежде чем переходить к доказательству, сформулируем такое следствие.

Следствие. В предположениях теоремы 1.32 либо А содержит наибольшее число, либо В содержит наименьшее число.

Действительно, если γ∈ А, то γ - наибольшее число в А; если γ∈В, то γ - наименьшее в В; в силу (а), одна из этих возможностей должна осуществиться, тогда как, в силу (b), они не могут осуществиться обе.

Именно существование γ (единственность тривиальна) составляет содержание этой важной теоремы. Оно показывает, что пробелы, которые мы обнаружили в системе рациональных чисел (ср. с примером 1.1), теперь заполнены. Более того, если бы мы попытались повторить тот процесс, который привел нас от рациональных чисел к вещественным, и начали строить сечения (как в определении 1.4), элементами которых были бы вещественные числа, то каждое сечение имело бы наименьшее верхнее число, и мы смогли бы сразу же отождествить каждое сечение с наименьшим из его верхних чисел, не получив ничего нового.

По этой причине теорему 1.32 иногда называют теоремой полноты для вещественных чисел.

Доказательство теоремы 1.32. Допустим, что имеются два числа γ₁ и γ₂, для которых выполнено заключение теоремы; пусть γ₁<γ₂. Выберем γ₃ так, что γ₁<γ₃<γ₂ (это возможно по теореме 1.29). Тогда из неравенства γ₃<γ₂ следует, что γ₃∈A, в то время как неравенство γ₁<γ₃ дает γ₃∈ В. Это противоречит условию (b). Таким образом, существует

не более чем одно число у с требуемыми свойствами.

Пусть γ - множество всех рациональных чисел р, таких, что р∈α при некотором α∈A. Мы должны проверить, что γ удовлетворяет условиям определения 1.4.

(I) Поскольку A непусто, γ также непусто. Если β∈ В и q∉β, то q∉α при любом α∈A (ибо α<β); значит, q∉γ.

(II) Если р∈γ и q<p, то p∈α при некотором α∈A; значит, q∈α, поэтому q∈γ.

(III) Если р∈γ, то р∈α при некотором α∈A; значит, существует q>p, такое, что q∈α; следовательно, q∈γ.

Таким образом, γ - вещественное число.

Ясно, что α≤γ при всех α∈A. Если бы при некотором β∈В оказалось, что β<γ, то нашлось бы рациональное число р, такое, что р∈ γ и р∉β; но если р∈ γ то р∈α при некотором α∈A, а отсюда следует, что β<α вопреки условию (d). Таким образом, γ≤β при всех β∈В, и доказательство закончено.

Теперь мы откажемся от некоторых соглашений об обозначениях, действовавших до сих пор. Буквы р, q, r, ... больше не будут предназначаться только для рациональных чисел, и буквами α, β, γ, ... тоже можно будет пользоваться для разных целей.

1.33. Определение. Пусть Е - некоторое множество вещественных чисел. Если существует число у, такое, что х≤у при всех х∈ Е, то мы будем говорить, что множество Е ограничено сверху, а число у будем называть верхней границей множества Е.

Нижние границы определяются аналогичным образом. Если множество Е ограничено сверху и снизу, то оно называется ограниченным.

1.34. Определение. Пусть Е ограничено сверху. Предположим, что у обладает следующими свойствами:

(a) у является верхней границей множества Е;

(b) если х<у, то х не является верхней границей множества Е.

Тогда у называется верхней гранью (точной верхней границей) множества Е (как следует из (b), существует не более чем одно такое число у). Мы будем употреблять сокращенное обозначение sup для верхней грани.

Нижняя грань (inf) любого множества Е, ограниченного снизу, определяется таким же образом.

1.35. Примеры.(а) Пусть множество Е состоит из всех чисел ¹/_n, где n = 1, 2, 3 ... . Тогда множество Е ограничено, его верхняя грань равна 1, а его нижняя грань равна 0. Заметим, что в этом случае верхняя грань принадлежит множеству, а нижняя грань-не принадлежит.

В общем случае верхняя грань (или нижняя грань) может принадлежать, а может и не принадлежать множеству.

(b) Пусть Е состоит из всех неотрицательных чисел. Тогда Е ограничено снизу, но не ограничено сверху, и его нижняя грань равна 0.

1.36. Теорема.Пусть Е - непустое множество вещественных чисел, ограниченное сверху. Тогда sup E существует.

Доказательство. Пусть А - множество вещественных чисел, определенное следующим образом: α∈A в том и только в том случае, когда существует число х∈Е, такое, что α<х. Пусть В состоит из всех вещественных чисел, не принадлежащих А.

Ясно, что никакой элемент множества А не является верхней границей множества Е, а каждый элемент множества В является верхней границей множества Е. Чтобы доказать существование верхней грани, достаточно поэтому доказать, что В содержит наименьшее число.

Проверим теперь, что А и В удовлетворяют предположениям теоремы 1.32.

Очевидно, что свойства (а) и (b) выполнены. Поскольку Е непусто, существует некоторый элемент х∈Е и каждое число α<х принадлежит A. Так как Е ограничено сверху, существует число у, такое, что х≤у при всех х∈ Е, значит, у∈В и выполнено свойство (с). Если α∈ A, то существует элемент х∈Е, такой, что α<x. Если β∈В, то х≤β. Таким образом, α<β при всех α∈A, β∈ В, и выполнено (d).

Итак, в силу следствия из теоремы 1.32, либо A содержит наибольшее число, либо В содержит наименьшее. Мы докажем, что первая возможность не может осуществиться.

Пусть α∈ A. Тогда существует число х∈ Е, такое, что α<х. Выберем α' так, что α<α'<x. Поскольку α'<x, то α'∈A, так что α не есть наибольшее число в A.

Это завершает доказательство.

В качестве приложения вышеизложенного мы приведем доказательство существования корней n-й степени из положительных вещественных чисел. Тем самым будет показано, как можно преодолеть трудности, отмеченные во введении (иррациональность ).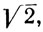

1.37. Теорема.Для всякого вещественного х>0 и всякого целого n>0 существует одно и только одно вещественное у>0, такое, что уⁿ = х.

Это число записывают так: 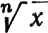или x^i/_n.

Доказательство. Единственность следует из того, что неравенство 0<y₁<y₂ влечет за собой неравенство y₁ⁿ<yⁿ₂.

Пусть Е - множество, состоящее из всех положительных вещественных t, таких, что tⁿ<x.

Если t = ^x/_(1+x), то 0<t<1; значит, tⁿ≤t<x, так что Е непусто.

Положим t₀ = 1 + х. Тогда из неравенства t>t₀ следует, что tⁿ≥t>x, поэтому t∉E и t₀ является верхней границей множества Е.

Пусть у - верхняя грань множества Е (которая существует по теореме 1.36).

Допустим, что уⁿ<x. Выберем h таким, что 0<h<1 и

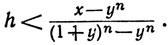
Тогда, обозначая через (ⁿ_m) коэффициент при z^m в разложении бинома (1+z)ⁿ, получим

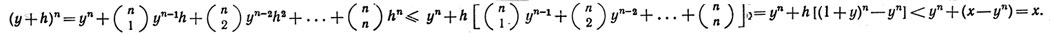
Таким образом, y + h ∈ E. Это противоречит тому, что у - верхняя граница множества Е.

Допустим, что у_n>х. Выберем k таким, что 0<k<1, k<y и

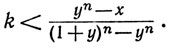
Тогда при t≥ y - k получим

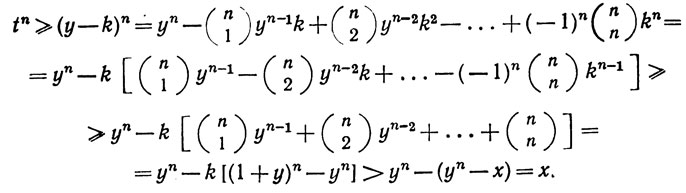
Таким образом, у - k является верхней границей множества E, а это противоречит тому, что y - наименьшая из верхних границ множества Е.

Следовательно, уⁿ = х.

1.38. Десятичные дроби. В заключение этого раздела укажем на соотношение между вещественными числами и десятичными дробями.

Пусть х>0 - вещественное число. Пусть n₀ - наибольшее целое число, такое, что n₀≤х. Если n₀, n₁,..., n_k-1 уже выбраны, то пусть n_k - наибольшее целое число, такое, что

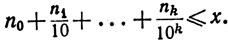
Пусть Е - множество чисел

(3)

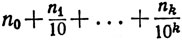
(k = 0, 1, 2,...).

Тогда х - верхняя грань множества Е. Десятичное разложение числа х имеет вид

(4) n₀, n₁, n₂, n₃,... .

Обратно, для любой бесконечной десятичной дроби (4) множество Е чисел вида (3) ограничено сверху^*, и (4) является десятичным разложением верхней грани этого множества^**.

^* (Необходимо отметить, что n_k≤9 (k = 1, 2, 3, ...).- Прим. перев.)

^** (Это утверждение автора следует уточнить. Десятичным разложением числа х названа последовательность чисел (3), полученная с помощью "приближений по недостатку", причем каждая конечная дробь, соответствующая последовательности n₀, n₁, ..., n_k, дает наилучшее приближение к х слева с точностью до 10^-k. Но в таком случае неверно, что дробь n₀, n₁, n₂, ..., n_k, ..., где n₀ = 0, n_k = 9 (k = 1, 2, ...) является десятичным разложением для sup E; таким десятичным разложением служит дробь 1,000....- Прим. перев.)

Мы не обсуждаем подробно десятичные дроби, так как никогда не будем ими пользоваться.