Дедекиндовы сечения

1.4. Определение. Множество а рациональных чисел называется сечением, если

(I) α содержит хотя бы одно рациональное число, но не всякое рациональное число;

(II) для р∈α и q<p (q - рациональное число) имеем q∈α;

(III) в α нет наибольшего числа.

В этом разделе мы будем употреблять буквы р, q, r, ... только для обозначения рациональных чисел; сечения будут обозначаться буквами α, β, γ, ... (за исключением случая, о котором говорится в определении 1.7).

1.5. Теорема.Если р∈α и q∉α, то p<q>

Доказательство. Если р∈α и q≤р, то из (II) следует, что q∈α.

Принимая во внимание эту теорему, элементы множества а иногда называют нижними числами сечения а, а рациональные числа, не принадлежащие а, называют верхними числами сечения а. Пример 1.1 показывает, что не всегда существует наименьшее верхнее число. Однако для некоторых сечений наименьшее верхнее число действительно существует.

1.6. Теорема.Пусть r - рациональное число. Пусть множество α состоит из всех рациональных чисел р, таких, что р<r. Тогда α - сечение, а r - наименьшее верхнее число сечения α.

Доказательство. Ясно, что α удовлетворяет условиям (I) и (II) определения 1.4. Что касается (III), то нужно лишь заметить, что для любого р∈α мы имеем

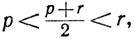
поэтому ^{(р + r)}/₂∈α.

Далее, r∉α. Поскольку неравенство р<r влечет за собой включение p∈α, то r - наименьшее верхнее число сечения α.

1.7. Определение. Сечение, построенное в теореме 1.6, называется рациональным сечением. Если мы захотим подчеркнуть, что α есть рациональное сечение, связанное с числом r указанным образом, то будем писать α=r^*.

1.8. Определение. Пусть α, β - сечения. Мы будем писать α = β, если из соотношения р∈α следует соотношение р∈β, а из q∈β следует q∈α, т. е. если эти два множества тождественно совпадают. В противном случае мы будем писать α≠β.

Замечание. Это определение на первый взгляд кажется излишним. Но равенство не всегда определяется как тождество. Например, если р = ^а/_b и q = ^c/_d - рациональные числа (а, b, с, d - целые), то р = q по определению означает, что ad = bc, но не обязательно а = с и b = d.

Введем теперь отношение порядка в множестве сечений.

1.9. Определение. Пусть α и β-сечения. Мы пишем α<β (или β>α), если имеется рациональное число р, такое, что р ∈β и р ∉α.

Если α>0*, то мы будем говорить, что сечение α положительно, если α≥0* - мы будем говорить, что оно неотрицательно. Аналогичным образом, если α<0*, то а отрицательно; оно неположительно, если α≤0*.

Мы, конечно, будем продолжать пользоваться символом < для рациональных чисел, так что этот символ (временно) будет нести двойную нагрузку. Однако из контекста всегда будет ясно, какой смысл следует ему приписать.

1.10. Теорема.Пусть α,β-сечения. Тогда либо α = β, либо α<, либо β&#

60;α.

Доказательство. Определения 1.8 и 1.9 ясно показывают, что если α = β, то ни одно из двух других отношений не выполнено. Чтобы показать, что отношения α<β и β<α исключают друг друга, предположим, что оба эти отношения имеют место. Поскольку α<β, имеется рациональное число р, такое, что

Поскольку β<α, имеется рациональное число q, такое, что

По теореме 1.5 из того, что р∈β и q∉β, следует, что q<p. Так как неравенства p<q и q<p не могут одновременно выполняться для рациональных чисел, мы пришли к противоречию.

До сих пор мы доказали, что из трех отношений может выполняться самое большее одно. Предположим теперь, что α≠β. Тогда два эти множества не совпадают тождественно; это значит, что либо α содержит рациональное р, не содержащееся в β, и в этом случае β<α, либо β содержит рациональное q, не содержащееся в α, и в этом случае α<β.

1.11. Теорема.Пусть α, β, γ-сечения. Если α<β и β<γ, то α?№60жγ.

Доказательство. Поскольку α<β, существует рациональное р, такое, что

Поскольку β<γ, существует рациональное q, такое, что

Теперь заметим, что из соотношений р∈β и q∉β следует, что p<q; последнее вместе с соотношением p∉α влечет за собой q∉α. Таким образом,

Это значит, что α<γ.

Последние две теоремы показывают, что отношение < между сечениями (определение 1.9) действительно обладает теми свойствами, которые обычно связывают с понятием неравенства.

Теперь мы переходим к построению арифметики в множестве сечений.

1.12. Теорема.Пусть α, β-сечения. Пусть γ-множество всех рациональных чисел r, таких, что r = p + q, где р∈α, q∈β. Тогда γ-сечение.

Доказательство. Мы покажем, что γ удовлетворяет трем условиям определения 1.4.

(I) Ясно, что γ непусто. Пусть s∉α, t∉β, s и t - рациональные числа. Тогда s + t > p + q при всех р∈α, q∈β, так что s + t ∉γ. Значит, γ содержит не все рациональные числа.

(II) Пусть r∈γ, s<r, s - рациональное число. Тогда r = p + q при некоторых р∈α, q∈β. Выберем рациональное t так, что s = t + q. Тогда t<р, значит, t∈α, поэтому s∈γ.

(III) Предположим, что г∈γ. Тогда r = p + q при некоторых р∈α, q∈β. Существует рациональное s>p, такое, что s∈α. Значит, s + q ∈γ и s + q ɚr, так что r не является наибольшим рациональным числом в γ.

1.13. Определение. Сечение γ, построенное в теореме 1.12, обозначается через α + β и называется суммой α и β.

(Замечание, сделанное после определения 1.9, относится также и к символу +.)

1.14. Теорема.Пусть α, β, γ-сечения. Тогда

(с) α + 0* = α.

Доказательство. Для построения α + β нужно взять множество всех рациональных чисел вида p + q (p∈α, q∈β). Для построения β + α вместо p + q нужно брать q + p. В силу закона коммутативности для сложения рациональных чисел, α + β и β + α - тождественные сечения, и свойство (а) доказано.

Аналогичным образом закон ассоциативности для сложения рациональных чисел влечет за собой равенство (b).

Чтобы доказать (с), выберем r∈α+0*. Тогда r = p + q при некоторых p∈α, q∈0* (т.е. q<0). Значит, p + q <p, так что p + q ∈α и r∈α.

Теперь пусть r∈α. Выберем рациональное число s>r, такое, что s∈α. Положим q = r - s. Тогда q<0, q∈0* и r = s + q, так что r∈α + 0*.

Таким образом, сечения α + 0* и α совпадают.

1.15. Теорема.Пусть α-сечение, и пусть задано рациональное число r>0. Тогда существуют рациональные р, q, такие, что p∈α, q∉α, q не является наименьшим из верхних чисел сечения α и q - р = r.

Доказательство. Выберем рациональное число s∈α. Для n = 0, 1, 2,... положим s_n = s + nr. Тогда имеется единственное целое m, такое, что s_m∈α и s_m+1∉α.

Если s_m+1 не есть наименьшее из верхних чисел сечения α, то выберем p = s_m, q = s_m+1.

Если s_m+1 - наименьшее из верхних чисел сечения α, то возьмем

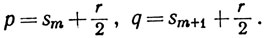
1.16. Теорема.Пусть α-сечение. Тогда существует одно и только одно сечение β, такое, что α + β = 0*.

Доказательство. Сначала мы докажем единственность. Если α + β₁ = α + β₂ = 0*, то теорема 1.14 показывает, что

Для доказательства существования обозначим через р множество всех рациональных р, таких, что - р является верхним числом сечения а, но не наименьшим из верхних чисел. Мы должны проверить, что это множество р удовлетворяет трем условиям определения 1.4. Выполнение условия (I) очевидно.

(II) Если р∈β и q<p (q-рациональное), то -р∉α и -q>-p, так что -q есть верхнее число сечения α, но не наименьшее. Значит, q∈β

(III) Если р∈β, то -р есть верхнее число сечения α, но не наименьшее, так что имеется рациональное число q, такое, что -q<-p и -q∉α. Положим

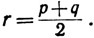
Тогда -q<-r<-р, так что -r есть верхнее число сечения α, но не наименьшее. Значит, мы нашли рациональное r>р, такое, что r∈β.

Показав, что β-сечение, мы должны теперь проверить, что α + β = 0*.

Предположим, что р∈ α + β. Тогда p = q + r при некоторых q∈α, r∈β. Значит, -r∉α, -r>q, q + r<0, и р∈0*.

Предположим, что р∈0*. Тогда р<. По теореме 1.15 имеются рациональные числа q∈α, r∉α (причем r не является наименьшим из верхних чисел сечения α), такие, что r - q = -р. Поскольку -r∈β, мы имеем

Доказательство закончено.

1.17. Определение. Сечение, построенное в теореме 1.16, обозначается -α.

1.18. Теорема.Для любых сечений α,β,γ, таких, что β<γ имеем α + β<α + γ. В частности (полагая β = 0*), мы имеем α + α>0*, если α>0*, γ>0*.

Доказательство. Согласно определениям 1.9 и 1.13, α + β≤α + γ. Если

то

по теореме 1.14.

1.19. Теорема.Пусть α, β-сечения. Тогда существует одно и только одно сечение γ, такое, что α + γ = β.

Доказательство. Единственность следует из того, что неравенство γ₁≠γ₂ влечет за собой неравенство α + γ₁≠α + γ₂ (теорема 1.18).

Положим γ = β + (-α). По теореме 1.14 мы имеем тогда

1.20. Определение. Сечение γ, построенное в теореме 1.19, обозначается через β - α, т. е. мы пишем β - α вместо β + (-α).

1.21. Замечание. Нам совсем не потребуется в этой книге теория групп. Однако читатели, знакомые с понятием группы, могли заметить, что теоремы 1.12, 1.14 и 1.16 означают, что множество сечений есть коммутативная группа относительно сложения, введенного определением 1.13. Сейчас мы определим умножение и покажем, что множество сечений образует поле.

Остановившись подробно на сложении и вычитании, мы совсем кратко и без доказательства рассмотрим умножение и деление. Доказательства теорем, которые мы далее сформулируем, совершенно аналогичны доказательствам теорем о сложении и вычитании, за исключением того, что иногда необходимо рассмотреть несколько случаев в зависимости от знака сомножителей.

1.22. Теорема.Пусть α, β -такие сечения, что α≥0*, β≥0*. Пусть γ состоит из всех отрицательных рациональных чисел и всех рациональных r, таких, что r = pq, где р∈ α, q∈β, р≥0, q≥0. Тогда γ - сечение.

1.23. Определение. Сечение, построенное в теореме 1.22, обозначается через αβ и называется произведением сечений α и β.

1.24. Определение. Каждому сечению α сопоставим сечение |α|, называемое абсолютной величиной α и определяемое следующим образом:

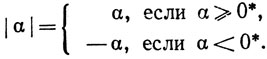
Ясно, что 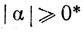при всех α и 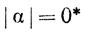тогда и только тогда, когда α = 0*.

Теперь мы можем дополнить определение умножения.

1.25. Определение. Пусть α, β-сечения. Положим, по определению,

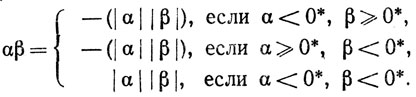
Заметим, что произведение |α| |β| уже было определено в 1.23, так как |α|≥0*, |β|≥0*.

1.26. Теорема. Для любых сечений α, β, γ имеем

(a) αβ = βα,

(g) если α<β и γ>0*, то αγ<βγ.

1.27. Теорема.Если α≠0*, то для любого сечения β существует одно и только одно сечение γ (которое мы будем обозначать через β/α), такое, что αγ = β.

В заключение этого раздела приведем три теоремы, касающиеся рациональных сечений.

1.28. Теорема.Для любых рациональных чисел р и q имеем

(c) р*<q* тогда и только тогда, когда p<q.

Доказательство. Если r∈ p* + q*, то r = s + t, где s<p, t<q, так что r< p + q. Значит, r∈(р + q)*. Если r∈(p + q)*, то r< p + q. Положим

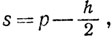
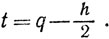
Тогда s∈p*, t∈q* и r = s + t, так что r∈ p* + q*.Этим доказано свойство (а). Доказательство свойства (b) аналогично.

Если р<q, то р∈ q*, но р∉ р*, так что р*<q*.

Если p*<q*, то имеется рациональное число r, такое, что r∈q*, r∉p*. Значит,

так что p<q.

1.29. Теорема.Если α, β-сечения и α<β, то существует рациональное сечение r*, такое, что α<r*<β.

Доказательство. Если а<β, то существует рациональное число р, такое, что р∈β, p∉α Выберем r>p так, что r∈β. Поскольку r∈β и r∉r*, мы видим, что r*<β.

Поскольку p∈r* и p∉α, мы видим, что α<r*.

1.30. Теорема.Для любого сечения α имеем p∈α тогда и только тогда, когда р*<α.

Доказательство. Для любого рационального р имеем р∉р*. Значит, р*<α, если р∈α. Обратно, если р*<α, то существует рациональное q, такое, что q∈α и q∉p*. Таким образом, q≥р; последнее неравенство вместе с q∈α влечет за собой включение р∈α.