Глава 1. Системы вещественных и комплексных чисел

Введение

Изучение основных понятий анализа (таких, как сходимость, непрерывность, дифференцирование и интегрирование) должно-основываться на точно определенном понятии числа. Мы, однако, не будем вступать в обсуждение аксиом, которым подчиняется арифметика целых чисел, а будем исходить из системы рациональных чисел.

Мы предполагаем, что читатель знаком с арифметикой рациональных чисел (т. е. чисел вида n/m, где n и m-целые, m≠0), и только напомним основные свойства этих чисел. Сумма, разность, произведение и частное любых двух рациональных чисел - рациональное число (деление на нуль исключается); выполняются законы коммутативности

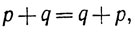
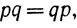
законы ассоциативности

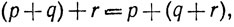
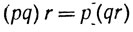
и закон дистрибутивности

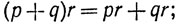
определено отношение <, задающее порядок в множестве рациональных чисел. Отношение < обладает тем свойством, что для любых рациональных чисел р и q либо p = q, либо p<q, либо q<p, оно транзитивно, т. е. если р<q и q<r, то р<r. Кроме того, р + q <0 и pq<0, если р<0 и q<0.

Хорошо известно, что система рациональных чисел обладает многими недостатками. Например, не существует рационального числа р, такого, что р² = 2 (мы это вскоре докажем). Это делает необходимым введение так называемых "иррациональных чисел", которые часто записываются в виде бесконечных десятичных разложений, причем соответствующие конечные десятичные дроби считаются их приближениями. Так, последовательность

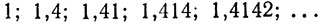
"стремится к 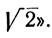Но до тех пор, пока мы не определили иррациональное число 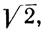остается открытым вопрос: к чему же все-таки стремится эта последовательность?

Главная цель этой главы и состоит в том, чтобы дать необходимое определение.

1.1.Пример. Сначала покажем, что никакое рациональное число р не удовлетворяет уравнению

Действительно, предположим, что это не так. Тогда существует удовлетворяющее уравнению (1) число p = m/n, где n, m - целые, причем хотя бы одно из них нечетно.

Подставляя в уравнение (1), получаем

ЭТО показывает, что m² -четное число. Значит, m четно (если бы т было нечетным, то и m² было бы нечетным) и, следовательно, m² делится на 4. Поэтому правая часть равенства (2) делится на 4, так что n² четно, откуда следует, что и n четно.

Таким образом, предположение о том, что выполнено равенство (1), заставляет нас заключить, что оба числа n, m-четные, вопреки нашему выбору n и m. Значит, равенство (1) невозможно при рациональном р.

Исследуем теперь подробнее эту ситуацию. Пусть А - множество всех положительных рациональных р, таких, что р²<2, и пусть множество В состоит из всех положительных рациональных р, таких, что р²>2. Мы покажем, что А не содержит наибольшего числа, а B не содержит наименьшего.

Точнее, мы докажем, что для любого р из А можно найти рациональное число q из А, такое, что р<q и для любого р из В мы можем найти рациональное число q из В, такое, что q<р.

Пусть р принадлежит А. Тогда р²<2. Выберем рациональное A, такое, что

и

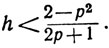
Положим q = p + h. Тогда q>p и

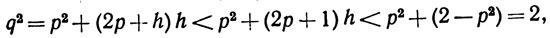
так что q находится в А. Этим доказана первая часть нашего утверждения.

Предположим теперь, что р принадлежит В. Тогда р²>2. Положим

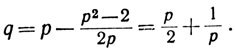
Тогда 0<q<p и

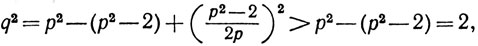
так что q принадлежит В.

1.2. Замечание. Цель приведенного выше рассуждения - показать, что в системе рациональных чисел имеются некоторые пробелы, несмотря на то что между любыми двумя рациональными числами находится третье [ибо p<^(p+q)/₂<q, если р<q]. Сейчас мы опишем предложенный Дедекиндом процесс, который позволяет заполнить эти пробелы и приводит нас к вещественным числам. Чтобы не увеличивать объема книги, мы не везде будем проводить рассуждения во всех деталях. Полное изложение, начинающееся с целых чисел, можно найти в книге Ландау "Основы анализа", где речь идет только об этой числовой системе.

1.3. Обозначения. Если A-множество (элементами которого могут быть числа или любые другие объекты), то запись х ∈А означает, что х принадлежит (или является элементом) А. Если х не является элементом A, мы будем писать х∉ А.

Множество, не содержащее ни одного элемента, мы будем называть пустым множеством. Если множество содержит хотя бы один элемент, то оно называется непустым.