Упражнения

1. Построить ограниченное множество вещественных чисел, имеющее ровно три предельные точки.

2. Построить компактное множество вещественных чисел, множество предельных точек которого счетно.

3. Пусть Е' - множество всех предельных точек некоторого множества E. Доказать, что Е' замкнуто.

4. Пусть 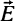= Е∪Е', где Е' определено выше. Чтобы получить 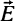, мы добавляем к Е все предельные точки Е; 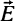называется замыканием множества Е. Доказать, что Е всегда замкнуто и что 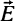⊂F, если Е⊂F и F замкнуто.

5. Корни любого уравнения

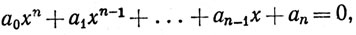
где а₀, ..., а_n - целые числа, называются алгебраическими числами. Доказать, что множество всех алгебраических чисел счетно.

Указание. При каждом положительном целом N существует только конечное число таких уравнений, что

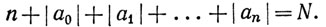
6. Дать пример открытого покрытия интервала (0,1), которое не содержит конечного подпокрытия.

7. Показать, что теорема 2.36 и ее следствие становятся неверными (в R¹, например), если слово "компактное" заменить словом "замкнутое" или "ограниченное".

8. Бывают ли бесконечные метрические пространства, не имеющие бесконечных компактных подмножеств?

9. Пусть X - пространство всех рациональных чисел, 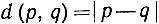и Е - множество всех рациональных р, таких, что 2<р²<3. Показать, что Е замкнуто и ограничено, но не компактно.

10. Метрическое пространство называется сепарабельным, если оно содержит счетное всюду плотное подмножество. Показать, что Rh сепарабельно.

Указание. Рассмотреть множество точек, все координаты которых рациональны.

11. Семейство {V_α} открытых подмножеств пространства X называется базой пространства X, если верно следующее: для каждого х∈Х и каждого открытого множества G, такого, что х∈G, имеем х∈V_α⊂G при некотором α. Иными словами, каждое открытое множество в X есть объединение некоторого подсемейства семейства {V_α}.

Доказать, что каждое сепарабельное метрическое пространство имеет счетную базу.

Указание. Возьмите все окрестности с рациональным радиусом и с центрами в некотором счетном всюду плотном подмножестве пространства X.

12. Пусть X - метрическое пространство, в котором каждое бесконечное подмножество имеет предельную точку.

Доказать, что X сепарабельно.

Указание. Зафиксируйте δ>0 и выберите x₁∈X. Выбрав х₁, ..., x_j∈, найдите, если это возможно, x_j+1∈X, такое, что d (x_i, x_j+1)≥δ для i = 1, ..., j. Покажите, что этот процесс должен закончиться после конечного числа шагов и что поэтому X можно покрыть конечным числом окрестностей радиуса δ. Возьмите δ = ¹/_n (n = 1, 2, 3, ...) и рассмотрите центры соответствующих окрестностей.

13. Пусть X - метрическое пространство, в котором каждое бесконечное подмножество имеет предельную точку.

Доказать, что X компактно.

Указание. Согласно упражнениям 11 и 12, X имеет счетную базу. Следовательно, каждое открытое покрытие пространства X содержит счетное подпокрытие {G_n}, n = 1, 2, 3, .... Если никакое конечное подсемейство семейства {G_n} не покрывает X, то дополнение F_n множества G₁∪...∪G_n непусто при каждом n, но пересечение ∩F_n - пусто. Пусть Е - множество, содержащее по точке из каждого F_n. Рассмотрите предельную точку множества Е и получите противоречие.

14. Доказать, что каждое замкнутое множество в сепарабельном метрическом пространстве есть объединение совершенного множества (может быть, пустого) и некоторого не более чем счетного множества. (Следствие: каждое счетное замкнутое множество в R^k имеет изолированные точки.)

15. Доказать, что каждое открытое множество в R¹ есть объединение не более чем счетного семейства попарно непересекающихся интервалов.

Указание. Воспользуйтесь упражнением 10.

16. Следуя доказательству теоремы 2.43, получить такой результат:

Если 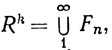где каждое F_n - замкнутое подмножество пространства R^k, то хотя бы одно F_n имеет непустую внутренность.

Эквивалентное утверждение. Если G_n - плотное открытое подмножество пространства R^k при k = 1, 2,3, ..., то 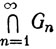непусто (на самом деле оно всюду плотно в R^k). (Это частный случай теоремы Бэра; см. общий случай в упражнении 17, гл. 3.)