3.5. Сопряжённые операторы

Пусть A - непрерывный линейный оператор, действующий в гильбертовом пространстве H. Зафиксировав y∈H, рассмотрим скалярное произведение f(x)=(Ax,y) как функционал относительно переменной x∈H. Оператор A линеен, то есть функционал линеен по переменной и ограничен, так как 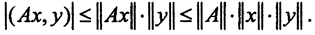По теореме Рисса о виде непрерывного линейного функционала, заданного в гильбертовом пространстве, имеет место равенство 9Ax,y)=(x,z). Здесь элемент однозначно определен элементом y и оператором A, то есть определяет некий оператор A^* как z=A^*y. Оператор А^* называется сопряженным с оператором А.

Определение 1. Оператор A^* называют сопряженным с оператором A. Другими словами, оператор A^* называется сопряжённым с оператором A, если ∀ x,y∈H скалярное произведение (Ax,y)=(x,A^*y). Оператор A называется самосопряжённым, если A=A^*, унитарным, если A^*=A^-1, и нормальным, если A^*A=AA^*.

Рассмотрим пространство H^*=L(H,R) непрерывных линейных функционалов, заданных на гильбертовом пространстве H и сопряженное с гильбертовым пространством H.

Определение 3. Последовательность {x_n} в гильбертовом пространстве H называется слабо сходящейся к элементу x∈H, если ∀f∈H^*{f(x_n)}→f(x), то есть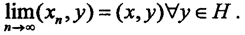

(Комментарий. 1. Значение функционала f∈H^* в точке x∈H обозначается как скалярное произведение f(x)=(f,x). Тогда сопряжённый оператор можно определить как f(Ax)=(f,Ax)=(A^*f,x). Но это просто обозначение, маскирующее отсутствие в B-пространствах скалярного произведения. Даже в конечномерном случае, когда имеет смысл скалярного произведения, вектор x∈H контравариантен, а f∈H^* вектор это вектор коэффициентов преобразований и он ковариантен. Эти векторы находятся в разных пространствах и по-разному преобразуются при смене системы координат.

2. Напомним, что сходимость по норме пространства носителей это обычная сходимость, когда x_n→x, то есть ||x_n-x||_n→∞→0. Её называют сильной. Если носителем является пространство C[a,b], то такая сходимость называется равномерной сходимостью. В пространстве непрерывных линейных операторов L(X,Y) сходимость ||A_n-A|||_n→∞→ 0 всегда называется равномерной сходимостью. Если же ∀x∈X 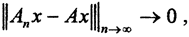то такая сходимость в пространстве L(X,Y) называется поточечной или сильной. Используя понятие сопряжённого пространства, в пространстве носителей можно ввести и другой тип сходимости, то есть другую топологию, а именно слабую сходимость. Но это, по сути, поточечная сходимость. Сильная сходимость влечёт слабую, так как |f(x_n)-f(x)|=|f(x_n-x)|≤||f||*||x_n-x||, и при 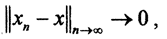то есть сильно,|f(x_n)-f(x)| → 0, то есть слабо. Обратное, вообще говоря, неверно. Пусть 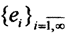базис в гильбертовом пространстве H и функционал f∈H^*. Из теоремы Рисса об общем виде функционала в гильбертовом пространстве, f(e_i)=(e_i,x) ∀x∈H. Ясно, что последовательность {e_i} не стремится к нулю, она даже не фундаментальна, так как ||e_i-e_j||²=2. Но по свойству коэффициентов Фурье последовательность {(e_i,x)}_i→∞→0, то есть слабо.)

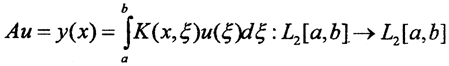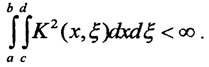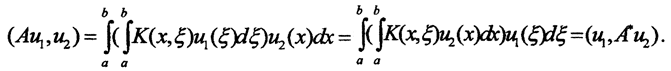Пример 1. Пусть оператор Фредгольма, где функция K(x,ξ), то есть ядро оператора A удовлетворяет условию Гильберта-Шмидта Тогда Но с другой стороны, 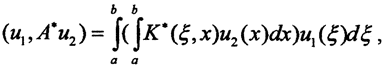то есть K^*(x,ξ)=K(x,ξ).

Итак, оператор A^* также является оператором Фредгольма с ядром K^*(x,ξ)=K(x,ξ) ∀x,ξ∈[a,b]. Если K(x,ξ)=K(ξ,x) ∀x,ξ∈[a,b], то ядро K(x,ξ) называется симметрическим. В этом случае, при L₂[a,b]→L₂[a,b], интегральный оператор является самосопряженным. Если ядро интегрального оператора не симметрическое, то оператор не самосопряжён.

Пример 2. Рассмотрим в пространстве Rⁿ оператор A:Rⁿ→Rⁿ, то есть Ax=y, причём x,y∈Rⁿ, x={x₁, x₂,...,x_n}, а 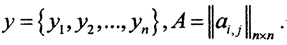. По определению (Ax,y)=(x,A^*y), то есть 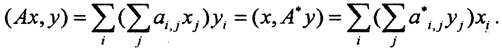Поменяв местами индексы, сразу получим, что a^*_i,j=a_j,i, то есть переход к сопряженному оператору в действительном n-мерном пространстве означает транспонирование матрицы этого оператора.

Пример 3. Показать, что если в гильбертовом пространстве H последовательность x_n слабо сходится к x и 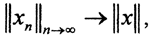то последовательность x_n сходится сильно.

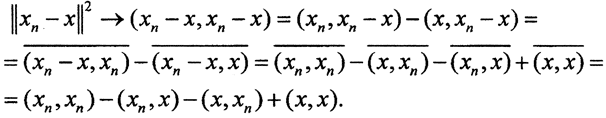
В силу непрерывности скалярного произведения ((x_n,x_n)-(x_n,x)-(x,x_n)+(x,x))|_n→∞→0 то есть 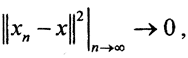что и означает сходимость по норме, то есть сильную сходимость.