3.6. Продолжения операторов и функционалов

Рассмотрим для определённости банаховы пространства. Если оператор определён не на всём банаховом пространстве X, а на линейном многообразии X'⊂X, то можно ли его продолжить на всё пространство, то есть можно ли построить новый оператор, совпадающий со старым на многообразии X'⊂X и сохраняющий какие-то его свойства на всём банаховом пространстве X? Для линейных операторов имеет место следующая теорема.

Теорема 1. Пусть A_X':X;→Y - непрерывный линейный оператор, заданный на всюду плотном линейном многообразии банахова пространства X'⊂X, где X,X' - банаховы пространства. Тогда существует непрерывный линейный оператор 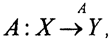причём ∀X' A_X'x=Ax, а нормы этих операторов совпадают, то есть ||A_X'||_X'=||A||_X.

Пусть x∈X, x∉X. Поскольку линейное многообразие всюду плотно в пространстве X, то ∃{x_n}→x, причём ∀x_n∈X' (по определению всюду плотного множества). То есть последовательность фундаментальна и ||A_X'x_n-A_X'x_m||≤||A_X'||*||x_n-x_m||_n,m→∞→0. Но тогда и последовательность {A_X'x_n} фундаментальна, а пространство банахово, то есть полное и поэтому последовательность {A_X'x_n}→y∈Y. Положив 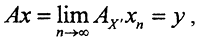мы определим некоторый оператор A.

Однако, линейный непрерывный функционал можно продолжить без изменения нормы, даже если он первоначально задан не на всюду плотном линейном многообразии банахова пространства.

Определение 1. Вещественный функционал p(x), заданный на вещественном линейном пространстве X, называется однородно-выпуклым (полунормой), если ∀x,y,∈X и &$8704;α>0 верно, что p(x+y)≤p(x)+p(y) и p(αx)=αp(x).

Определение 2. Пусть функционал f(x) задан на линейном многообразии L⊂X, где X - линейное нормированное пространство. Вещественный функционал F(x) есть продолжение функционала f(x), если F(x)=f(x) ∀x∈L⊂X.

Теорема 1 (Принцип продолжения Хана-Банаха). Пусть линейный непрерывный функционал f(x) задан на линейном многообразии L⊂X, где X - линейное нормированное пространство, причём на линейном нормированном пространстве X задан однородно-выпуклый функционал p(x):f(x)≤p(x)∀x∈L⊂X. Тогда функционал f(x) можно продолжить на всё пространство X, причём для продолжения F(x) выполнено, что F(x)≤p(x)∀x∈X.

Пусть x₀∈X, x₀∉L. Для любого действительного t рассмотрим множество L₁ = {y∈X:y=x+tx₀}.

1. Покажем, что это множество есть линейное многообразие, причём любой элемент из него имеет однозначное представление.

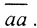
Пусть для любого действительного t существует элемент y∈X, имеющий два представления y=x₁+t₁x₀ и y=x₂+t₂x₀. Если t₁=t₂, то и x₁=x₂. Если t₁≠t₂, то x₁+t₁x₀=x₂+t₂x₀ ⇒(x₁-x₂)=(t₁-t₂)x₀, то есть 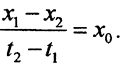Но x₁,x₂∈L₁, тогда и x₁-x₂ ∈L₁, и левая часть принадлежит L₁, но x₀&38713;L₁. Очевидно, что L₁ есть линейное многообразие, так как ∀y₁,y₂∈L₁, λ₁,λ₂∈R, имеем (λ₁x₁+λ₂x₂)+(λ₁t₁+λ₂t₂)x₀=x₃+t₃x₀∈L₁.

2. Сформулируем требования, которым должен удовлетворять функционал f(x), чтобы его продолжение удовлетворяло неравенству F(x)≤p(x). Пусть каким-то образом удалось получить продолжение функционала f(x)∈L на L₁, причём так, что выполняются условия теоремы:

1. ∀x∈L выполнено f(x)=F(x),

2. ∀x∈ выполнено F(x)≤p(x).

Тогда ∀y∈L₁ можно записать, что ∀y∈f₁(y)=f₁(x+tx₀)=f₁(x)+tf₁(x₀)=f₁(x)+tC=f(x)+tC, где C - значение функционала в точке x₀, а f₁(x)=f(x) ∀x∈L. Тогда любой линейный функционал, продолжаемый с линейного многообразия на линейное многообразие L₁ должен иметь вид f₁(y)=f(x)+tC, где C - константа. Но для того, чтобы сохранялись свойства, надо показать, что f₁(y)=f(x)+tC≤p(x+tx₀). Рассмотрим два случая.

1) Пусть t>0. Разделив на t>0, получим 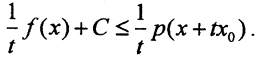Тогда в силу линейности функционала f(x), 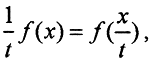а из первого свойства полунормы 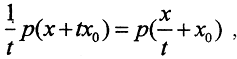то есть 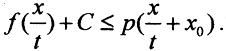Так как t - произвольное, то 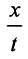- произвольный элемент из t. Обозначив его через x, сразу получим ∀x∈L C≤p(x+x₀)-f(x).

2) Пусть t<0. Разделив неравенство f₁(y)=f(x)+tC≤p(x+tx₀) на -t, получим 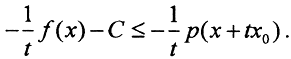Обозначим -^x/_t=y. Теперь f(^x/_-t)-C≤p(^x/_-t-x₀), то есть C≥f(y)-p(y-x₀). Итак, если мы хотим, чтобы продолжение удовлетворяло неравенству F(x)≤p(x), нужно показать, что ∀x,y∈L константу С, определяющую продолжение, всегда можно выбрать так: f(y)-p(y-x₀)≤C≤p(x+x₀)-f(x).

Рассмотрим ∀x,y∈L соотношение f(x)+f(y)=f(x+y)≤p(x+y)=p(x+x₀+y-x₀)≤p(x+x₀)+p(y-x₀). Отсюда следует, что f(y)-p(y-x₀)≤p(x+x₀)-f(x). Так как это условие выполняется ∀x,y∈L, в том числе и для супремума и инфинума, то 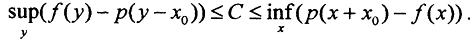Таким образом, константу С, удовлетворяющую условию теоремы, следует выбрать так: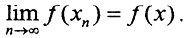

3) Опишем завершение доказательства. Если X - сепарабельное банахово пространство, то в нём существует счётное всюду плотное множество {x₀, x₁, x₂,...,x_n,...}. Матиндукцией осуществляем продолжение, последовательно присоединяя к L те элементы, которых там нет. В результате мы получим продолжение функционала на всюду плотное линейное многообразие 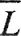=X. Дальше, как указано в комментарии, продолжение функционала осуществляется по непрерывности: ∃{x_n}→x, причём все x_n∈L, x∈X, 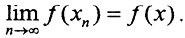Если пространство не сепарабельно, но банахово, то доказательство завершается методом трансфинитной индукции, обобщающим метод математической индукции на несчётные множества.

Примерно в этом месте в основном и заканчивается ликбез и начинается то, что математики называют функциональным анализом и его приложениями.