
3.4. Пространства функционалов
Определение 1. Линейным функционалом в гильбертовом пространстве H называется линейный оператор, отображающий H во множество чисел (вещественных или комплексных).
Поскольку линейный функционал является оператором, то для него определено понятие непрерывности, нормы и справедливы все свойства операторов.
Определение 2. Ядром линейного функционала f, определенного в H, называется совокупность всех векторов x∈H, для которых f(x)=0. Ядро функционала f обозначается через ker f.
Теорема 1. Если f - линейный функционал в H, то ker f является подпространством в H.
Надо показать, что ker f является замкнутым линейным многообразием.
1. Покажем, что любая линейная комбинация произвольных двух векторов лежит x,y ∈ker f в ker f. Но если x,y ∈ker f, то f(x)=f(y)=0, а значит, для любых чисел α,β имеем f(αx+βy)=αf(x)+βf(y)=0. Следовательно, αx+βy ∈ker f.
2. Рассмотрим произвольную сходящуюся последовательность векторов из ∈ker f, {xn}n→∞→x0∈H. Поскольку линейный функционал f непрерывен, то 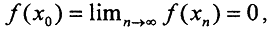 а значит, .Следовательно, ядро f замкнуто.
а значит, .Следовательно, ядро f замкнуто. 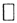
Определение 3. Коразмерностью подпространства S называется размерность его ортогонального дополнения S⊥.
Теорема 2. Коразмерность ядра ненулевого непрерывного функционала f равна единице.
Гильбертово пространство H может быть представлено в виде прямой суммы замкнутого подпространства S и его ортогонального дополнения S⊥: S+S⊥=H. Это означает, что для любого вектора x∈H найдутся, и притом единственным образом, векторы y∈S и z∈S⊥ такие, что x=y+z. Поскольку функционал f непрерывен, то его ядро ker f замкнуто и, следовательно, все пространство H представляется в виде прямой суммы ядра ker f и его ортогонального дополнения (ker f)⊥: H=ker f  (ker f)⊥. Последнее означает, что каждый вектор x∈H может быть единственным образом представлен в виде x=x1+x2, где x1∈ker f, а x2∈(ker f)⊥. С другой стороны, функционал f не равен нулю, а значит H≠ker f. Следовательно, ортогональное дополнение к ядру содержит не только нулевой вектор. Пусть x2∈(ker f)⊥ и x2≠0. Рассмотрим произвольный вектор x3∈(ker f)⊥ и положим
(ker f)⊥. Последнее означает, что каждый вектор x∈H может быть единственным образом представлен в виде x=x1+x2, где x1∈ker f, а x2∈(ker f)⊥. С другой стороны, функционал f не равен нулю, а значит H≠ker f. Следовательно, ортогональное дополнение к ядру содержит не только нулевой вектор. Пусть x2∈(ker f)⊥ и x2≠0. Рассмотрим произвольный вектор x3∈(ker f)⊥ и положим 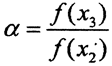 и y=αx2-x3. Тогда, с одной стороны, y∈(ker f)⊥, так как вектор y является линейной комбинацией векторов x2∈(ker f)⊥ и x3∈(ker f)⊥. Но с другой стороны вектор y∈(ker f), так как f(y) = f(αx2-x3)=αf(x2)-f(x3)=0. Следовательно, вектор y=ker f∩(ker f)⊥. Поэтому y=0 и αx2=x3. Таким образом, любой вектор из (ker f)⊥ пропорционален вектору x2. Это и означает, что коразмерность ядра равна единице.
и y=αx2-x3. Тогда, с одной стороны, y∈(ker f)⊥, так как вектор y является линейной комбинацией векторов x2∈(ker f)⊥ и x3∈(ker f)⊥. Но с другой стороны вектор y∈(ker f), так как f(y) = f(αx2-x3)=αf(x2)-f(x3)=0. Следовательно, вектор y=ker f∩(ker f)⊥. Поэтому y=0 и αx2=x3. Таким образом, любой вектор из (ker f)⊥ пропорционален вектору x2. Это и означает, что коразмерность ядра равна единице.
Теорема 3. Если ядро функционала замкнуто, то он непрерывен.
Если ядро функционала совпадает со всем пространством, то функционал равен нулю и, очевидно, непрерывен. Если ядро функционала f является замкнутым подпространством, не совпадающим со всем пространством H, то ортогональное дополнение к ядру содержит хоть один ненулевой вектор w∈(ker f)⊥. Произвольным образом выберем последовательность {xn}n→∞→0, ∀xn∈H. Поскольку H=ker f  (ker f)⊥, а значит для каждого номера n найдутся векторы yn∈ker f и zn∈(ker f)⊥ такие, что xn=yn+zn. Далее, каждый из векторов zn представим в виде zn = αnw. Норма
(ker f)⊥, а значит для каждого номера n найдутся векторы yn∈ker f и zn∈(ker f)⊥ такие, что xn=yn+zn. Далее, каждый из векторов zn представим в виде zn = αnw. Норма 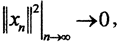 но
но 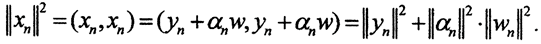 Сумма двух неотрицательных слагаемых в пределе равна нулю, а вектор w ненулевой, причём
Сумма двух неотрицательных слагаемых в пределе равна нулю, а вектор w ненулевой, причём 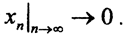 Следовательно
Следовательно 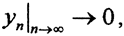
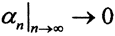 и f(xn) = f(yn+αnw)=f(yn)+αnf(w)=αnf(w)→0=f(0) при n→∞. Значит, линейный функционал f непрерывен в нуле и поэтому непрерывен всюду.
и f(xn) = f(yn+αnw)=f(yn)+αnf(w)=αnf(w)→0=f(0) при n→∞. Значит, линейный функционал f непрерывен в нуле и поэтому непрерывен всюду. 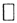
Определение 4. Множество непрерывных линейных функционалов, определенных в гильбертовом пространстве H, называется пространством, сопряженным с H, и обозначается через H*. Очевидно, что H* - линейное пространство.
Теорема 4 (теорема Рисса об общем виде линейного непрерывного функционала). Пусть H - гильбертово пространство. Тогда для всякого непрерывного линейного функционала f на H существует единственный вектор x0∈H такой, что f(x)=(x,x0) ∀x∈H, причем ||f||=||x0||.
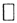
Пусть вектор x0∈H существует. Скалярное произведение линейно по первому аргументу, поэтому при любом x0∈H формула определяет линейный функционал на H. Из неравенства Буняковского Коши следует, что |f(x)|=|(x,x0)|≤||x||*||x0||,то есть норма f не превосходит ||x0||, а значит, функционал f непрерывен. Однако, |f(x)|=|(x,x0)|=||x0||2 и, следовательно, ||f||=||x0||. Покажем теперь, что вектор x0∈H существует и единственен. 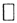
Существование.
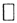
Поскольку функционал f непрерывен, то его ядро замкнуто и все пространство H представляется в виде: H=ker f  (ker f)⊥. Стало быть ∀x∈H существует и единственно представление x=x1+x2, где x1∈ ker f, а x2∈(ker f)⊥. Если f(x)=0, то ker f = H, (ker f)⊥={0}, и, положив x0 = 0 сразу получим f(x)=0=(x,x0) ∀ x∈H. Если f(x) ≠0, то ker f ≠H и ортогональное дополнение к ядру (ker f)⊥≠{0} имеет размерность 1. Пусть вектор x3(ker f)⊥, ||x3||=1, что для любого вектора x2∈(ker f)⊥ найдется число α такое, что x2=αx3, а значит, для любого вектора ∀ x∈H найдутся вектор x1∈ker f и число α такие, что x=x1+αx3. Стало быть, ∀ x∈H имеем f(x) = f(x1+αx3)=f(x1)+αf(x3)=αf(x3). Тогда, учитывая, что (x1,x3)=0, а ||x3||=1, получим
(ker f)⊥. Стало быть ∀x∈H существует и единственно представление x=x1+x2, где x1∈ ker f, а x2∈(ker f)⊥. Если f(x)=0, то ker f = H, (ker f)⊥={0}, и, положив x0 = 0 сразу получим f(x)=0=(x,x0) ∀ x∈H. Если f(x) ≠0, то ker f ≠H и ортогональное дополнение к ядру (ker f)⊥≠{0} имеет размерность 1. Пусть вектор x3(ker f)⊥, ||x3||=1, что для любого вектора x2∈(ker f)⊥ найдется число α такое, что x2=αx3, а значит, для любого вектора ∀ x∈H найдутся вектор x1∈ker f и число α такие, что x=x1+αx3. Стало быть, ∀ x∈H имеем f(x) = f(x1+αx3)=f(x1)+αf(x3)=αf(x3). Тогда, учитывая, что (x1,x3)=0, а ||x3||=1, получим 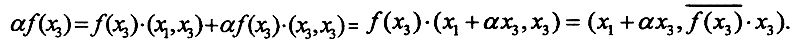 Обозначив
Обозначив 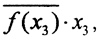 сразу получим f(x)=(x,x0)
сразу получим f(x)=(x,x0) 
Единственность вектора x0.
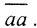
Допустим, что нашлось два вектора x01≠x02:∀x∈H (x,x01)=(x,x02)=f(x). Тогда для всех ∀x∈H имеем (x,x01-x02)=0. Полагая в последнем равенстве x=x01-x02, получим 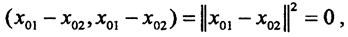 а значит x01=x02.
а значит x01=x02. 
(Комментарий. Из теоремы Рисса следует, что правило, которое сопоставляет вектору x0∈H непрерывный линейный функционал f по формуле f(x) =(x,x0) определяет линейный изоморфизм векторных пространств H и H*. Следовательно, H и H* "с точностью до обозначений" являются одним и тем же пространством.)
Пример. Норма функционала f:R22→R равна 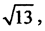 а его значение в точке (1,1) равно -1. Найти значение f в точке (7,8).
а его значение в точке (1,1) равно -1. Найти значение f в точке (7,8).
В соответствии с теоремой Рисса существует элемент a∈R22:(x,a)=f(x), причём 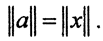 Но
Но 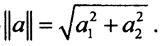 Таким образом, сразу получаем симметрическую систему для определения
Таким образом, сразу получаем симметрическую систему для определения 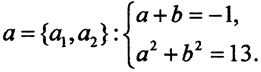
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'