3.3.2. Корректность компактных операторов

Определение. Линейный оператор A, отображающий банахово пространство E в себя (или другое банахово пространство), называется компактным (вполне непрерывным), если каждое ограниченное множество он переводит в предкомпактное.

(Комментарий. Напомним, что множество M метрического пространства X компактно, если из любого бесконечного его подмножества можно выделить последовательность, сходящуюся к элементу из M, и предкомпактно, если замыкание компактно. Если линейный оператор компактен, то он переводит любую ограниченную последовательность {x_n} в компактную последовательность {Ax_n}, то есть из любой подпоследовательности последовательности {Ax_n} можно выделить сходящуюся подпоследовательность. Компактность и предкомпактность это прежде всего свойства пространств. Суть компактности в исчерпываемости некого бесконечномерного пространства конечномерным приближением с любой наперед заданной точностью. Компактный оператор наследует свойства конечномерного оператора в том смысле, что всегда может быть приближен им.)

Теорема 1. Компактный оператор A всегда ограничен.

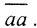
Пусть компактный оператор A не ограничен. Тогда найдется последовательность {x_n}, такая, что ||Ax_n||≥n. Но тогда из неё нельзя выделить сходящуюся подпоследовательность, что противоречит тому, что A - вполне непрерывный оператор.

Комментарий. Не любой непрерывный линейный оператор вполне непрерывен. Рас (смотрим, например, единичный оператор I:L₂[a,b]→L₂[a,b]:Ix=x ∀x∈L₂[a,b]. Он, очевидно, ограничен, но не компактен. Покажем это.)

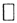
В пространстве L₂[a,b] существует бесконечная ортонормированная система (ОНС) 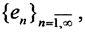такая, что 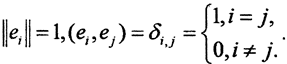Ясно, что последовательность {e_n} лежит на сфере 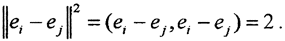, то есть она ограничена, но из неё нельзя выделить сходящуюся подпоследовательность, так как 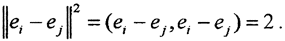Значит, единичная сфера S(0,1) в гильбертовом пространстве - замкнутое и ограниченное множество, но не компакт, а IS(0,1)=S(0,1). Таким образом, единичный оператор I не компактен.

Можно показать, что единичный оператор I в любом бесконечномерном банаховом пространстве B не компактен. Это следует из теоремы Рисса о некомпактности единичного шара в бесконечномерном B-пространстве.

Теорема 2. Если A - компактный оператор,B - ограниченный в банаховом пространстве X, то операторы AB и BA - компактны.

Если множество M⊂X ограничено, то множество BM тоже ограничено. Следовательно, множество ABM предкомпактно, а это и означает, что оператор AB компактен. Далее, если M⊂X ограничено, то AM предкомпактно, а тогда в силу непрерывности B множество BAM тоже предкомпактно, то есть оператор BA компактен.