3.3. Обратный оператор

Определение 1. Пусть X и Y - линейные пространства. Линейный оператор A:X→Y называется обратимым, если уравнение Ax=y имеет единственное решение. Совокупность всех векторов y∈Y, для каждого из которых существует вектор x∈X, такой, что Ax=y, называется образом оператора A (множеством значений оператора A) и обозначается ImA или R(A).

(Комментарий. Множество Im(A) значений оператора A может, вообще говоря, и не совпадать со всем пространством Y.)

Определение 2. Совокупность всех векторов x∈X, на которых оператор A определён, называется областью определения оператора A и обозначается DomA или D(A).

Определение 3. Если оператор A обратим, то каждому вектору y∈ ImA сопоставляется единственный вектор x∈X, являющийся решением уравнения Ax=y. Оператор, осуществляющий это соответствие, называется обратным к A и обозначается A^-1.

Если существует обратный оператор A^-1, то решение задачи записывается в явном виде: x=A^-1y. То есть необходимо найти элемент x∈X, если задан элемент y∈Y. Ясно, что важное значение приобретает выявление условий, при которых обратный оператор существует и ограничен.

(Комментарий. Множество L⊂E, где Е - линейное пространство, называется линейным многообразием, если ∀x,y∈L и ∀λ∈R x+y ∈L, λx∈L, то есть содержит все линейные комбинации входящих в него векторов. В линейной алгебре чаще используют термин "линейное подпространство". Множество M = x₀+L, где x₀∈E, L - линейное многообразие, называется аффинным многообразием. В частности, M является линейным подпространством тогда и только тогда, когда М содержит нулевой элемент. Множество значений оператора есть линейное многообразие в Y. В самом деле, пусть y₁∈ImA и y₂∈ImA. Тогда найдутся векторы x₁, x₂∈X, такие, что Ax₁=y₁ и Ax₂=y₂. Поэтому для любых чисел α₁,α₂ верно, что A(α₁x₁+α₂x₂)=α₁Ax₁+α₂Ax₂=α₁y₁+α₂y₂, то есть вектор (α₁y₁+α₂y₂)∈ImA. Ясно, что D(A^-1)=R(A), R(A^-1)=D(A).)

Теорема 1. Пусть оператор A:X→Y линеен и существует A^-1. Тогда A^-1 тоже линеен.

Для произвольных y₁,y₂∈Y, α₁,α₂∈R обозначим x = A^-1(α₁y₁+α₂y₂)-α₁A^-1y₁-α₂A^-1y₂. Тогда Ax = A(A^-1(α₁y₁+α₂y₂)-α₁A^-1y₁-α₂A^-1y₂) = α₁y₁+α₂y₂-α₁y₁-α₂y₂ = 0. Теперь A^-1Ax = x = 0 ⇒(A^-1(α₁y₁+α₂y₂)=α₁A^-1y₁+α₂A^-1y₂.

Определение 4. Ядром оператора A называется множество ker A = N(A) = {x∈D(A):A(x) = 0}. Очевидно, что N(A) не пусто, так как 0∈N(A).

Определение 5. Оператор A называется вырожденным, если N(A)≠{0}.

Теорема 2. Пусть X и Y линейные конечномерные пространства, а оператор A линейный. Обратный оператор A^-1 существует тогда и только тогда, когда оператор A невырожденный.

Достаточность.

Пусть оператор A невырожденный, т.е. Ax=0 ⇔ x=0 (нуль-пространство, ядро оператора A тривиально). Тогда для любых двух элементов x₁≠x₂ имеем A(x₁-x₂)≠0 ⇔ Ax₁ͰAx₂, то есть оператор A взаимно однозначный, а значит, существует обратный оператор A^-1.

Необходимость.

Пусть оператор A имеет обратный оператор A^-1. Заметим, что A^-1 - линейный оператор (теорема 1) и докажем что оператор A - невырожденный. Пусть это не так, то есть существует x≠0 такой, что Ax=0. Тогда 0≠x=A^-1Ax = A^-1(Ax) = A^-10 = 0. Полученное противоречие показывает, что Ax=0 ⇔ x=0, то есть оператор A - невырожденный.

(Комментарий. В доказательстве теоремы не участвует размерность пространства. Однако она верна только в конечномерном случае, то есть в конечномерном пространстве оператор A обратим, если и только если N(A)={0}. В бесконечномерном пространстве это, вообще говоря, не так. Например, множество всех ограниченных последовательностей x = {x₁, x₂, x₃,...,x_i,...} с операциями покоординатного сложения и умножения на скаляр образует линейное пространство. Определим на нём оператор сдвига Ax = A(x₁, x₂, x₃,...,x_i,...) = {0,x₁, x₂, x₃,...,x_i,...}. Ясно, что Ker A = 0 (Ax = 0 только при x ={0,0,0,...,0,...}). Однако этот оператор не имеет обратного. В самом деле, пусть оператор A^-1 существует и A^-1x = y. Рассмотрим вектор x={1,0,0,...,0,...}. Тогда (AA^-1)x=x=A(A^-1x)=Ay. Но первая координата вектора x=Ay всегда равна нулю, а должна быть равна единице.)

Нас интересует не только разрешимость уравнения Ax=y, но и непрерывная зависимость решения от правой части уравнения, то есть корректность уравнения.

Теорема 3. (Критерий непрерывности обратного оператора.) Пусть X и Y - линейные нормированные пространства. Оператор A^-1 существует и непрерывен на R(A), если и только если ∃m>0:∀x∈D(A) и выполняется неравенство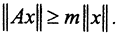

Необходимость. Пусть обратный оператор A^-1 существует и ограничен на R(A). Тогда существует такая постоянная M, что 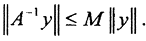Обозначая y=Ax и 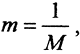сразу получаем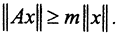

Достаточность. Из того факта, что 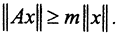следует, что уравнение Ax=0 имеет единственное решение x=0. В самом деле, пусть Ax=0. Тогда 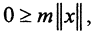то есть 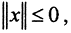а значит x=0. Тогда из теоремы 2 следует существование обратного оператора A^-1. Полагая в этом неравенстве x=A^-1y, сразу получим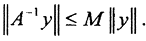

Определение 6. Пусть X и Y - линейные нормированные пространства. Оператор А называется непрерывно обратимым, если 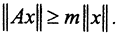, причём A^-1⊂L(X,Y), R(A)=Y.

Определение 7. Задача решения уравнения Ax=y корректно разрешима по Адамару, если:

2) решение x˜=A^-1y˜ того же уравнения с возмущённой правой частью таково, что 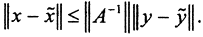Это означает, что малое изменение правой части y влечет малое изменение решения.

(Комментарий. Если линейный оператор А непрерывно обратим, то задача решения уравнения Ax=y корректно разрешима по Адамару.)

В случае существования непрерывного оператора A∈L(X,Y) имеет место следующая теорема:

Теорема 4. (Теорема Банаха о гомеоморфизме). Пусть X→^AY, где A - биективный непрерывный линейный оператор, X,Y - банаховы пространства и R(A)=Y. Тогда существует линейный непрерывный обратный оператор A^-1.

Из биективности отображения следует однозначная разрешимость уравнения Ax=y для любой правой части, то есть существование обратного оператора A^-1. Его линейность следует из теоремы 1. Непрерывность же обратного оператора следует из принципа открытых отображений Банаха: оператор A, как непрерывный оператор, любое открытое множество переводит в открытое. Тогда для оператора A^-1 его прообраз R(A)=Y открыт. Тогда, в соответствии с критерием непрерывности, оператор A^-1 непрерывен.

(Комментарий. Таким образом, если A - биективный непрерывный линейный оператор, такой, что X→^AY, где X,Y - банаховы пространства, и R(A) = Y, то задача решения уравнения Ax=y корректно разрешима по Адамару.)