
3.2. Непрерывность линейных операторов
Пусть X и Y - нормированные пространства и А: X→Y, где А - линейный оператор, всюду заданный в X (т.е. D(A) = X).
Определение 1. Линейный оператор А, заданный всюду в банаховом пространстве X и со значениями в банаховом пространстве Y называется непрерывным в точке x0∈D(A), если . Эквивалентное определение непрерывности оператора в точке:
Определение 2. Линейный оператор А, заданный всюду в банаховом пространстве X и со значениями в банаховом пространстве Y называется непрерывным в точке , если для любой последовательности xn, n=1, 2, …, ∀xn∈D(A), xn→x0, последовательность Axn сходится к Ax0.
Определение 3. Оператор A называется непрерывным на D(A), если он непрерывен в каждой точке.
Теорема 1. Линейный оператор А, заданный всюду в банаховом пространстве X и со значениями в банаховом пространстве Y непрерывен тогда и только тогда, когда он непрерывен в нуле.
Необходимость.
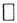
Ясно, что если оператор А непрерывен в каждой точке, то он непрерывен в нуле. 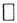
Достаточность.
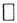
Пусть оператор A непрерывен в нуле и {xn}→x0. Тогда {xn-x0}→0, а так как оператор A непрерывен в нуле и линеен, то {A(xn-x0)} = {A(xn)-A(x0)}→0. 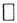
Определение 4. Линейный оператор А называется непрерывным, если он непрерывен в точке x = 0.
Теорема 2. Пусть А: X→Y, А - линейный оператор, X,Y - банаховы пространства. Для того чтобы линейный оператор А был непрерывным, необходимо и достаточно, чтобы он был ограниченным.
Необходимость.
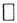
Пусть оператор А ограничен. Покажем, что он непрерывен. Достаточно доказать непрерывность А в нуле. Рассмотрим любую последовательность {xn}→0, то есть ||xn-x0||→0. Тогда ||Axn-A0||→0, то есть ||Axn||<c||xn||→0), так как оператор А ограничен, а {xn}→0, то есть A{xn}→0, то есть оператор А непрерывен в нуле. 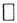
Достаточность.
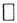
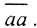
Допустим, что оператор А не ограничен. Это значит, что числу 1 найдется хотя бы один соответственный вектор x1 такой, что ||Ax1||>1||x1||. Числу 2 найдется вектор x2, такой, что ||Ax2||>2||x2|| и т.д. Числу n найдется вектор xn, такой, что ||Axn||>n||xn||. Теперь рассмотрим последовательность векторов 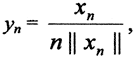 где
где 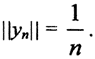 Следовательно, последовательность yn →0 при n →∞. Так как оператор А непрерывен в нуле, то Аyn →0, однако
Следовательно, последовательность yn →0 при n →∞. Так как оператор А непрерывен в нуле, то Аyn →0, однако 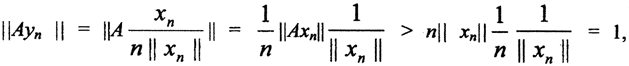 получаем противоречие с тем, что Аyn →0, то есть оператор А - ограничен.
получаем противоречие с тем, что Аyn →0, то есть оператор А - ограничен. 
(Комментарий. Для линейных операторов понятия ограниченности и непрерывности оператора эквивалентны. Непрерывные линейные операторы будем обозначать аббревиатурой НЛО.)
Пример 1. Рассмотрим оператор Фредгольма в пространстве L2[a,b], сопоставляющий функции u(x) новую функцию Au = f(x), определенную с помощью формулы 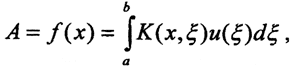 где K(x,ξ) - некоторая фиксированная непрерывная функция двух переменных. Оператор A называется интегральным, его линейность очевидна из линейности интеграла. Если ядро K(x,ξ) непрерывно по совокупности аргументов, то в соответствии с теоремой о непрерывной зависимости от параметра собственного интеграла, оператор A действует в линейном пространстве функций.
где K(x,ξ) - некоторая фиксированная непрерывная функция двух переменных. Оператор A называется интегральным, его линейность очевидна из линейности интеграла. Если ядро K(x,ξ) непрерывно по совокупности аргументов, то в соответствии с теоремой о непрерывной зависимости от параметра собственного интеграла, оператор A действует в линейном пространстве функций.
1. Покажем, что оператор Фредгольма ограничен, а, следовательно, непрерывен при действии C[a,b]→C[a,b]. Полагаем ядро K(x,ξ) непрерывным в квадрате [0,1]*[0,1], то есть ограниченным. При этом K0 = max|K(x,ξ)|, а норма ||u(ξ)|| = max|u(ξ)| = 1. Тогда 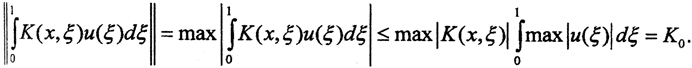
2. Покажем, что оператор Фредгольма ограничен и, следовательно, непрерывен в пространстве L2[a,b]. По неравенству Коши-Буняковского для каждого фиксированного x∈[0,1], полагая, что 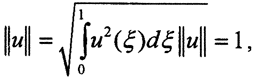 можно записать
можно записать  Интегрируем по x:
Интегрируем по x: 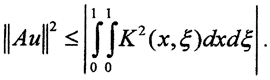 Правая часть неравенства не зависит от u и ограничена, поэтому
Правая часть неравенства не зависит от u и ограничена, поэтому 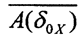
Ранее было показано, что отображение топологических пространств непрерывно, если и только если прообраз всякого открытого множества открыт. В частности, если отображение непрерывно, то прообраз всякого открытого множества открыт. Однако, если оператор, осуществляющий отображение, линеен, то ситуация значительно лучше.
Теорема 3 (Принцип открытости отображений Банаха). Пусть A:X→Y - линейный непрерывный оператор,X,Y - банаховы пространства. Тогда образ любого открытого множества в пространстве X есть открытое множество в пространстве Y.
Лемма 1. Пусть A:X→Y - линейный непрерывный оператор,X,Y - банаховы пространства. Тогда для любой окрестности нуля δ0X в пространстве X замыкание образа этой окрестности 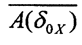 содержит в себе некоторую окрестность нуля ε0Y в пространстве Y, то есть
содержит в себе некоторую окрестность нуля ε0Y в пространстве Y, то есть 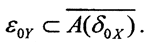

Открытая окрестность нуля δ0X в пространстве X содержит в себе некий открытый шар B(0,δ)⊂ δ0X. Зададим δ>0 и рассмотрим последовательность 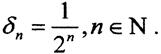 . Тогда для любого фиксированного n
. Тогда для любого фиксированного n 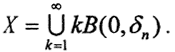 . То есть любой вектор x∈kB(0,δn), где k - наименьшее из целых чисел, больших
. То есть любой вектор x∈kB(0,δn), где k - наименьшее из целых чисел, больших 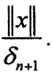 Оператор А сюръективен, то есть
Оператор А сюръективен, то есть 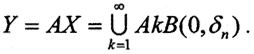 По условию Y - банахово пространство, которое по теореме Бэра о категориях есть множество второй категории. Это значит, что его нельзя представить в виде объединения счётного числа нигде не плотных множеств. Другими словами, существует номер k0 = k(n) и открытое множество AMk0, такие, что найдётся шар k0AB(0,δn), который будет плотным в открытом множестве AMk0, то есть k0AB(0,δn)⊂ AMk0, но множество AMk0 будет содержаться в замыкании шара
По условию Y - банахово пространство, которое по теореме Бэра о категориях есть множество второй категории. Это значит, что его нельзя представить в виде объединения счётного числа нигде не плотных множеств. Другими словами, существует номер k0 = k(n) и открытое множество AMk0, такие, что найдётся шар k0AB(0,δn), который будет плотным в открытом множестве AMk0, то есть k0AB(0,δn)⊂ AMk0, но множество AMk0 будет содержаться в замыкании шара 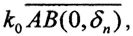 или шар
или шар 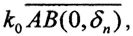 будет содержать в себе некоторое открытое множество
будет содержать в себе некоторое открытое множество 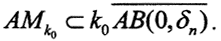 Можно сказать, что замыкание шара
Можно сказать, что замыкание шара 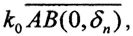 имеет непустую открытую внутренность AMk0. Так как оператор А непрерывен, то соответствующее множество в пространстве X, множество k0Mk0 тоже будет открыто, как и множество
имеет непустую открытую внутренность AMk0. Так как оператор А непрерывен, то соответствующее множество в пространстве X, множество k0Mk0 тоже будет открыто, как и множество 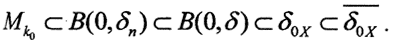 С другой стороны, множество AMk0 и есть окрестность нуля в пространстве Y, то есть можно считать, что AMk0 = ε0Y. Тогда сразу
С другой стороны, множество AMk0 и есть окрестность нуля в пространстве Y, то есть можно считать, что AMk0 = ε0Y. Тогда сразу 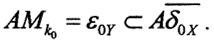

Лемма 2. Пусть A:X→Y - линейный непрерывный оператор,X,Y - банаховы пространства. Тогда для любой окрестности нуля δ0X в пространстве X, образ этой окрестности A(δ0X) содержит в себе некоторую окрестность нуля ε0Y в пространстве Y, то есть ε0Y⊂A(δ0X).

Открытая окрестность нуля δ0X в пространстве X содержит в себе некий открытый шар 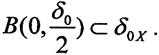 Возьмём произвольную последовательность
Возьмём произвольную последовательность 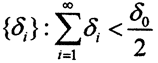 и обозначим BX(0,δi) открытые шары радиусов δi, а BY(0,εi) - открытые шары радиусов εi. В силу только что доказанной леммы
и обозначим BX(0,δi) открытые шары радиусов δi, а BY(0,εi) - открытые шары радиусов εi. В силу только что доказанной леммы 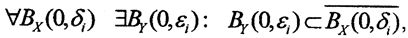 причём последовательность {εi} = {ε0, ε1, ε2,...,εn...} монотонно убывает. Пусть y∈BY(0,ε0). Так как
причём последовательность {εi} = {ε0, ε1, ε2,...,εn...} монотонно убывает. Пусть y∈BY(0,ε0). Так как 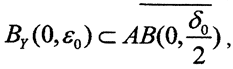 то найдётся точка
то найдётся точка 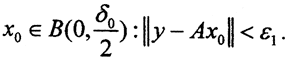 Так как
Так как 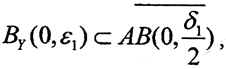 то найдётся точка
то найдётся точка 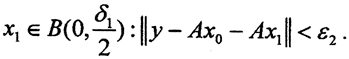 И так далее. Таким образом,
И так далее. Таким образом, 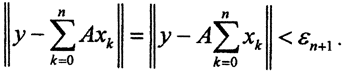 Пусть
Пусть 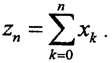 Оценим норму
Оценим норму 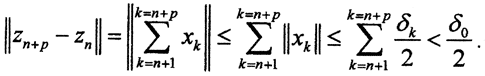 Это значит, что последовательность {zn} фундаментальна в пространстве X. Так как пространство X полное, то она сходится, то есть существует элемент
Это значит, что последовательность {zn} фундаментальна в пространстве X. Так как пространство X полное, то она сходится, то есть существует элемент 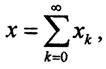 такой, что
такой, что 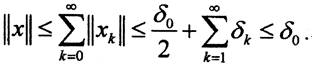 Тогда, в силу соотношения
Тогда, в силу соотношения  имеем
имеем 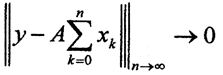 и
и 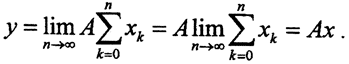 Таким образом, мы фактически показали, что образ A(δ0X) любой окрестности нуля δ0X в пространстве X содержит в себе некоторую окрестность нуля ε0Y в пространстве Y, то есть ε0Y⊂A(δ0X)
Таким образом, мы фактически показали, что образ A(δ0X) любой окрестности нуля δ0X в пространстве X содержит в себе некоторую окрестность нуля ε0Y в пространстве Y, то есть ε0Y⊂A(δ0X) 
Теперь легко доказать принцип открытости отображений Банаха.

Нулевой элемент пространства X - такой же элемент пространства X, как и все остальные. То есть если M⊂X - произвольное открытое множество в пространстве X, то ∀x∈X ∃δ⊂M. Обозначим через δ0X такую окрестность нуля, что её сдвиг на x, то есть x+δ0X окажется внутри δ: x+δ0X∈δ. Так как ε0Y⊂A(δ0X), то A(x+δ0X) = Ax+Aδ0X⊂Ax+ε0Y. В силу произвольности теорема доказана. 
Определение 5. Взаимно однозначные и взаимно непрерывные отображения F:X→Y из топологического пространства X в топологическое пространство Y называются гомеоморфизмами.
Определение 6. Если существует гомеоморфизм F:X→Y, то говорят, что X и Y гомеоморфны друг другу.
(Комментарий. В этом случае мы можем наложить X на Y без самопересечений и разрывов, приклеивая x∈X к F(x)⊂Y. Так что получается, что X и Y устроены одинаково.
Понятие гомеоморфизма являются центральным для многих разделов топологии, в которых изучаются характеристики, описывающие гомеоморфные, то есть одинаково устроенные пространства, и поэтому их можно считать разными экземплярами одного и того же объекта.)
(Комментарий. Поскольку норма это число, то множество операторов должно быть замкнуто относительно обычных алгебраических операций. Но будет ли оно пространством, то есть можно ли на этом множестве определить операцию предельного перехода, и если да, то будет ли это пространство полным? Обозначим множество всех непрерывных линейных операторов, действующих из пространства X в пространство Y, через L(X,Y). Очевидно, L(X,Y) - линейное пространство.)
Теорема 4. Пространство L(X,Y) есть нормированное пространство с нормой 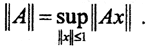

Достаточно проверить для 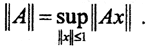 аксиомы нормы.
аксиомы нормы. 
Определение 5. Последовательность линейных непрерывных операторов ({An}∈L(X,Y) сходится равномерно к оператору A∈L(X,Y), если ∀ε<0 ∃N = N(ε)>0:(∀n>N, ∀x из шара 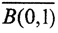 верно, что ||Anx-Ax||<ε. Это обозначают как ||An-A|||n→∞→0.
верно, что ||Anx-Ax||<ε. Это обозначают как ||An-A|||n→∞→0.
Теорема 5. Если X есть нормированное пространство, a Y банахово, то пространство L(X,Y) банахово в смысле равномерной сходимости.

Надо показать, что существует непрерывный линейный оператор A, который является пределом равномерно сходящейся последовательности операторов An.
1. Покажем существование непрерывного оператора 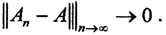 Рассмотрим произвольную фундаментальную последовательность {An}∈L(X,Y). Для любого элемента x∈X последовательность {Anx} фундаментальна, так как
Рассмотрим произвольную фундаментальную последовательность {An}∈L(X,Y). Для любого элемента x∈X последовательность {Anx} фундаментальна, так как 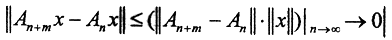 и m>0. Пространство Y банахово, то есть найдётся
и m>0. Пространство Y банахово, то есть найдётся  Таким образом, каждому элементу x∈X мы поставили в соответствие единственный элемент
Таким образом, каждому элементу x∈X мы поставили в соответствие единственный элемент 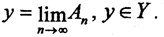 Оператор A линеен, так как линейны операторы An.
Оператор A линеен, так как линейны операторы An.
2. Покажем, что оператор A, являющийся пределом для последовательности операторов An, непрерывен. В самом деле, так как последовательность {An} фундаментальна в L(X,Y), то последовательность норм {||An||} ограничена, то есть ||An||≤m. С другой стороны, 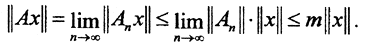 Таким образом, ||A||≤m, и, следовательно, оператор A является непрерывным. В силу фундаментальности последовательности операторов
Таким образом, ||A||≤m, и, следовательно, оператор A является непрерывным. В силу фундаментальности последовательности операторов 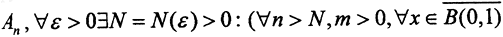
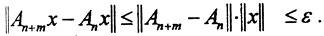 Перейдем в данном неравенстве к пределу при m→∞. Тогда ∀ε>0 ∃N=N(ε)>0:∀n>N при условии
Перейдем в данном неравенстве к пределу при m→∞. Тогда ∀ε>0 ∃N=N(ε)>0:∀n>N при условии 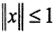 выполнится
выполнится 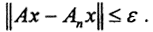 Это значит, что
Это значит, что 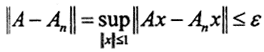 при всех n>N то есть
при всех n>N то есть 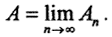

(Комментарий. В пространство линейных непрерывных операторов можно ввести и другие типы сходимости. Рассмотрим последовательность операторов ортогонального проецирования в гильбертовом пространстве. Пусть 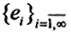 есть некоторый ортонормированный базис в гильбертовом пространстве l2: e1 ={1,0,0,...}, e2 ={0,1,0,...},...,, и так далее. Тогда произвольный элемент x∈X⊂l2 представим в виде ряда Фурье
есть некоторый ортонормированный базис в гильбертовом пространстве l2: e1 ={1,0,0,...}, e2 ={0,1,0,...},...,, и так далее. Тогда произвольный элемент x∈X⊂l2 представим в виде ряда Фурье 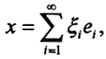 где ξi =(x,ei). Определим оператор проецирования Pn на подпространство l2, натянутое на первые n элементов базиса, как
где ξi =(x,ei). Определим оператор проецирования Pn на подпространство l2, натянутое на первые n элементов базиса, как 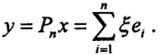 Тогда
Тогда 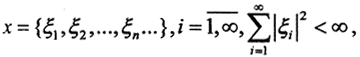 а Pnx = {η1, η2,...,ηn}. То есть ηi = ξi, i=1,n, ηi = 0, i>n. Тогда
а Pnx = {η1, η2,...,ηn}. То есть ηi = ξi, i=1,n, ηi = 0, i>n. Тогда 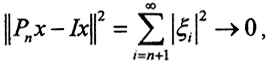 как остаток сходящегося ряда, где I - тождественный оператор. То есть Pn→i, но это какая-то другая сходимость, потому что равномерной сходимости нет. В самом деле, как только n>N, то
как остаток сходящегося ряда, где I - тождественный оператор. То есть Pn→i, но это какая-то другая сходимость, потому что равномерной сходимости нет. В самом деле, как только n>N, то 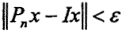 для любого x. Пусть x = en+1. Тогда
для любого x. Пусть x = en+1. Тогда 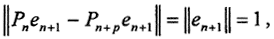 так как Pn не сохраняет en+1, а Pn+p сохраняет. Это рассуждение подводит нас к следующему определению.)
так как Pn не сохраняет en+1, а Pn+p сохраняет. Это рассуждение подводит нас к следующему определению.)
Определение 6. Последовательность операторов {An}∈L(X,Y) называется поточечно (сильно) сходящейся к оператору A∈L(,Y), если ∀x∈X 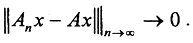
(Комментарий. Поточечная сходимость означает сходимость в каждой точке пространства. Мы показали, что поточечная (сильная) сходимость последовательности операторов не влечет за собой, вообще говоря, равномерной сходимости этих же операторов. Обратное всегда верно: равномерная сходимость последовательности операторов всегда влечет за собой поточечную. Действительно, 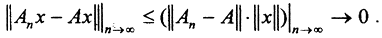
Будет ли пространство L(X,Y) банаховым и в смысле поточечной сходимости? Покажем, что будет.)
Теорема 6 (Принцип равномерной ограниченности Банаха-Штейнгауза). Пусть X,Y - банаховы пространства, а последовательность {An}∈L(X,Y) есть последовательность непрерывных линейных операторов, множество значений которых ограничено в любой точке x∈X, то есть 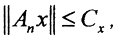 , где Cx - константы, быть может, различающиеся от точки к точке. Тогда числовая последовательность норм этих непрерывных линейных операторов
, где Cx - константы, быть может, различающиеся от точки к точке. Тогда числовая последовательность норм этих непрерывных линейных операторов 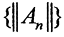 тоже ограничена, то есть ∀n∈N верно, что
тоже ограничена, то есть ∀n∈N верно, что 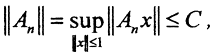 где константа C есть общая константа, то есть речь идёт об равномерной ограниченности.
где константа C есть общая константа, то есть речь идёт об равномерной ограниченности.

Покажем сначала, что если 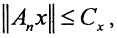 то в замкнутом шарe
то в замкнутом шарe  (0,1) последовательность {Anx} ограничена ∀x∈
(0,1) последовательность {Anx} ограничена ∀x∈ (0,1), то есть
(0,1), то есть 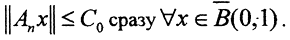
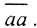
Пусть последовательность {An}∈L(X,Y) не ограничена ни в каком замкнутом шаре. Тогда она не ограничена и в шаре 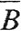 (0,1), равно как и в шаре
(0,1), равно как и в шаре 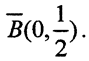 Это значит, что существует элемент
Это значит, что существует элемент 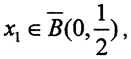 , на котором, начиная с номера n1, норма
, на котором, начиная с номера n1, норма 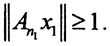 Но оператор An1 непрерывен, то есть это соотношение выполняется и в некотором замкнутом шаре
Но оператор An1 непрерывен, то есть это соотношение выполняется и в некотором замкнутом шаре 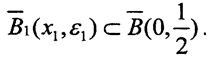 Тогда для этого шара
Тогда для этого шара 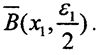 последовательность {Anx} не ограничена и в шаре
последовательность {Anx} не ограничена и в шаре 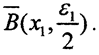 То есть существует элемент
То есть существует элемент  на котором, начиная с номера n2, норма
на котором, начиная с номера n2, норма 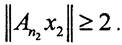 Снова это неравенство выполняется и в некотором замкнутом шаре
Снова это неравенство выполняется и в некотором замкнутом шаре 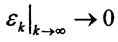 Ясно, что существует точка
Ясно, что существует точка 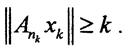 , которая принадлежит всем шарам при условии, что
, которая принадлежит всем шарам при условии, что 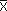 и в которой
и в которой  Но это противоречит условию
Но это противоречит условию 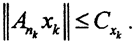 То есть в замкнутом шаре
То есть в замкнутом шаре 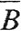 (0,1) последовательность {Anx} ограничена ∀x∈
(0,1) последовательность {Anx} ограничена ∀x∈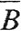 (0,1), то есть
(0,1), то есть 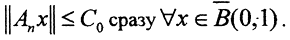 Но тогда норма
Но тогда норма 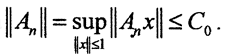

Теорема 7. Пусть X и Y - банаховы пространства. Тогда пространство L(X,Y) банахово в смысле поточечной сходимости.

Рассмотрим фундаментальную последовательность {Anx}. Если последовательность {Anx} фундаментальна в каждой точке x∈X, а пространство Y банахово, то она сходится в этой точке, то есть существует {Anx}n→∞→Ax, то есть она ограничена, и ограничен, а следовательно, линеен оператор A, то есть 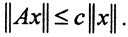 Это как раз и означает, что любая поточечно сходящаяся фундаментальная последовательность непрерывных линейных операторов сходится к непрерывному линейному оператору, то есть пространство L(X,Y) банахово в смысле поточечной сходимости.
Это как раз и означает, что любая поточечно сходящаяся фундаментальная последовательность непрерывных линейных операторов сходится к непрерывному линейному оператору, то есть пространство L(X,Y) банахово в смысле поточечной сходимости. 
Определение 7. Пусть A - оператор, вообще говоря, нелинейный, A:X→X, где (X,ρ) - полное метрическое пространство. Оператор A называется сжимающим если существует константа q:q∈(0,1), такая, что для любых x1, x2 ∈X имеет место неравенство 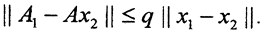
(Комментарий. Всякое сжимающее отображение непрерывно.

Пусть ∀ε>0 0<δ≤ε тогда как только 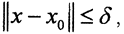 имеем:
имеем: 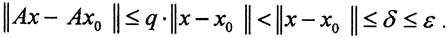 Таким образом, оператор A непрерывен.
Таким образом, оператор A непрерывен.  )
)
Определение 8. Элемент называется неподвижной точкой оператора A, если Ax=x.
Теорема 7 (Принцип сжимающих отображений Банаха). Сжимающее отображение A:X→X полного метрического пространства (X,ρ) в себя имеет единственную неподвижную точку 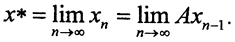
Существование. Пусть точка x0∈X. Составим последовательность {xn}:x1 =Ax0, x2 = Ax1,...,xn=Axn-1 и покажем, что она фундаментальна. Так как ρ(x1,x2)≤λρ(x0,x1), ρ(x2,x3)=ρ(Ax1,Ax2)≤λρ(x1,x2)≤λ2ρ(x0,x1) и так далее, тогда ρ(xn,xn+1)≤λnρ(x0,x1). Последовательно применяя неравенство треугольника, получим
Пусть точка x0∈X. Составим последовательность {xn}:x1 =Ax0, x2 = Ax1,...,xn=Axn-1 и покажем, что она фундаментальна. Так как ρ(x1,x2)≤λρ(x0,x1), ρ(x2,x3)=ρ(Ax1,Ax2)≤λρ(x1,x2)≤λ2ρ(x0,x1) и так далее, тогда ρ(xn,xn+1)≤λnρ(x0,x1). Последовательно применяя неравенство треугольника, получим 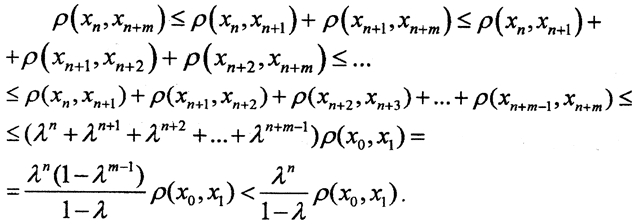
Так как λ<1, то 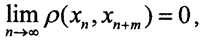 то есть последовательность {xn} фундаментальна. А поскольку метрическое пространство (X,ρ) полное, то {xn}→x*. Покажем, что Ax*=x*. Так как ∀ε>0∃N=N(ε):∀n>N выполнено
то есть последовательность {xn} фундаментальна. А поскольку метрическое пространство (X,ρ) полное, то {xn}→x*. Покажем, что Ax*=x*. Так как ∀ε>0∃N=N(ε):∀n>N выполнено 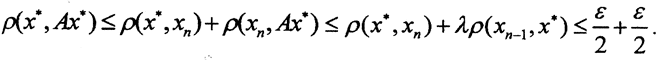
Отображение A:X→X непрерывно, то есть, переходя к пределу, получим 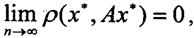 то есть x* = Ax*.
то есть x* = Ax*. 
Единственность.
 . Пусть x1*≠x2* - две неподвижные точки. Тогда ρ(x1*,x2*)>0 но ρ(x1*,x2*) = ρ(Ax1*,Ax2*) ≤λρ(x1*,x2*)⇒λ≥1.
. Пусть x1*≠x2* - две неподвижные точки. Тогда ρ(x1*,x2*)>0 но ρ(x1*,x2*) = ρ(Ax1*,Ax2*) ≤λρ(x1*,x2*)⇒λ≥1. 
(Комментарий. Неверно считать, что для применения принципа сжатых отображений достаточно, чтобы ρ(Ax, Ay)<ρ(x,y). Рассмотрим, например, функцию 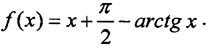 Если функция f(x), x∈R, имеет ограниченную производную, |f'(x)|≤λ<1, то отображение f будет сжимающим. В самом деле, по теореме Лагранжа, ∀x1, x2 ∈[a,b] и∀ξ∈(a,b) получим |f(x1)-f(x2)| = |f'(ξ)|*|x1-x2|≤λ|x1-x2|, λ∈(0,1). (Условие |f(x1)-f(x2)|≤λ|x1-x2| называется условием Липшица.) В нашем случае
Если функция f(x), x∈R, имеет ограниченную производную, |f'(x)|≤λ<1, то отображение f будет сжимающим. В самом деле, по теореме Лагранжа, ∀x1, x2 ∈[a,b] и∀ξ∈(a,b) получим |f(x1)-f(x2)| = |f'(ξ)|*|x1-x2|≤λ|x1-x2|, λ∈(0,1). (Условие |f(x1)-f(x2)|≤λ|x1-x2| называется условием Липшица.) В нашем случае 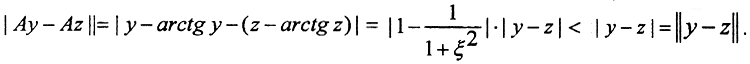 Но
Но 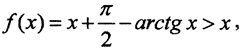 что и означает отсутствие неподвижной точки у этой функции. Функция f(x) не удовлетворяет теореме о неподвижной точке.)
что и означает отсутствие неподвижной точки у этой функции. Функция f(x) не удовлетворяет теореме о неподвижной точке.)
Примеры. 1. Рассматривая преобразования Rn2→Rn2, Rn1→Rn1 и Rn∞→Rn∞ мы получили выражения для их норм: 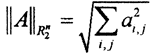 (эвклидова),
(эвклидова), 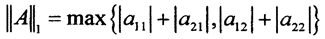 (столбиковая) и
(столбиковая) и 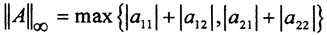 (строчная). Ели они меньше единицы, то соответствующие отображения сжимающие.
(строчная). Ели они меньше единицы, то соответствующие отображения сжимающие.
2. Решить уравнение f(x) = 0.
Определяем границы корней, то есть участки, на которых функция f(x) меняет знак. Пусть при x∈[a,b] функция f(x) меняет знак. Далее, рассмотрим функцию φ(x) = x-αf(x). Ясно, что если φ(x) = x, то f(x) = 0, следовательно φ(x) = x ⇔f(x) = 0. Выбираем параметр α так, чтобы |φ'(x)| = |1-αf'(x)|<1, тогда αf'(x)∈(0,2) ∀x∈[a,b].
3. Решить уравнение x3-9x2+30x-22=0.

На сегменте x∈[0,3] рассмотрим уравнение 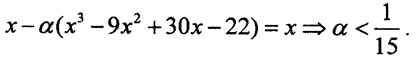 Положим α=0,03, x0 = 2. Корень x=1.
Положим α=0,03, x0 = 2. Корень x=1.
4. При каких λ оператор Фредгольма  является сжимающим
является сжимающим
а) при действии C[0,1]→C[0,1];
б) при действии L2[0,1]→L2[0,1].
а) Рассмотрим две непрерывные функции y(x), z(x)∈C[0,1]. Тогда
Рассмотрим две непрерывные функции y(x), z(x)∈C[0,1]. Тогда 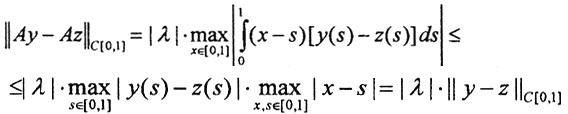 и оператор А: C[0,1]→C[0,1] будет сжимающим при |λ|<1.
и оператор А: C[0,1]→C[0,1] будет сжимающим при |λ|<1. 
б) Рассмотрим две непрерывные функции y(x), z(x)∈L2[0,1], тогда
Рассмотрим две непрерывные функции y(x), z(x)∈L2[0,1], тогда  и оператор А: L2[0,1]→L2[0,1] будет сжимающим при
и оператор А: L2[0,1]→L2[0,1] будет сжимающим при 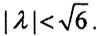 .
.
5. При каких λ оператор Вольтерра 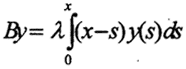 является сжимающим
является сжимающим
а) при действии C[0,1]→C[0,1];
б) при действии L2[0,1]→L2[0,1].
а) Рассмотрим две непрерывные функции y(x), z(x)∈C[0,1],
Рассмотрим две непрерывные функции y(x), z(x)∈C[0,1], 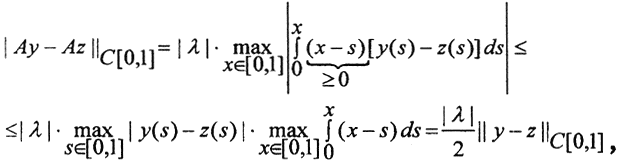 тогда и оператор В: C[0,1]→C[0,1] будет сжимающим при |λ|<2.
тогда и оператор В: C[0,1]→C[0,1] будет сжимающим при |λ|<2. 
б) Рассмотрим две непрерывные функции y(x), z(x)∈L2[0,1], тогда
Рассмотрим две непрерывные функции y(x), z(x)∈L2[0,1], тогда 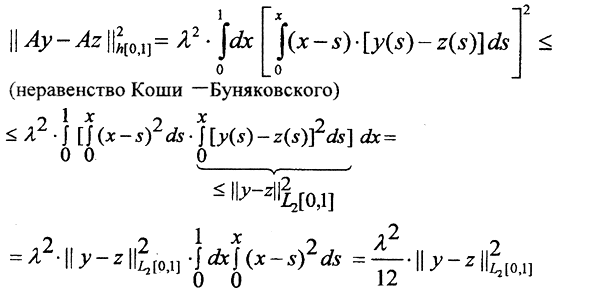 и оператор В: L2[0,1]→L2[0,1] будет сжимающим при
и оператор В: L2[0,1]→L2[0,1] будет сжимающим при 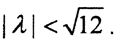

|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'