III. Пространства операторов

3.1. Определение линейного оператора

Пусть X и Y - нормированные пространства, оба вещественные или оба комплексные или линейные топологические пространства.

Определение 1. Линейным оператором, действующим из пространства X в пространство Y, называется отображение A:X→Y или Ax = y или Au = f (если u∈U, f∈F, где U и F - пространства функций), удовлетворяющее условию A(λ₁x₁+λ₂x₂) = λ₁Ax₁+λ₂Ax₂, где ∀λ₁,λ₂∈R, ∀x₁, x₂∈ X.

Пример 1. Пусть I:X→X по правилу Ix = x ∀x∈X, то есть оператор I переводит каждый вектор пространства X в себя. Ясно, что A(λ₁x₁+λ₂x₂) = λ₁Ax₁+λ₂Ax₂. Это единичный оператор. Соответственно, нулевой оператор 0x = 0 ∀x∈X переводит каждый вектор пространства X в нулевой вектор пространства Y.

(Комментарий. Те, кто считает, что слово единица пишется через "E", единичный оператор обозначают буквой E. Символ 0 теперь может означать либо число нуль, либо нулевой вектор пространства X, либо нулевой вектор пространства Y, либо нулевой оператор, действующий из пространства X в пространство Y.)

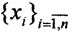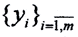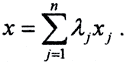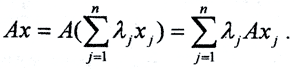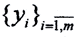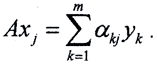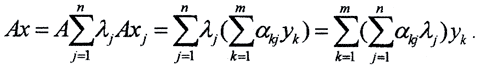Пример 2. Пусть X,Y - конечномерные эвклидовы пространства, базис в пространстве X, а базис в пространстве Y. Тогда ∀x∈X верно, что Оператор A линеен, то есть Но каждый из векторов Ax_j лежит в пространстве Y и поэтому может быть разложен по базису : Тогда Совокупность чисел 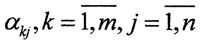называется матрицей оператора A. Совокупность чисел 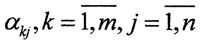называется матрицей оператора A. То есть каждому оператору A соответствует некоторая матрица α_kj и наоборот, каждой матрице 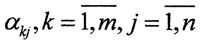соответствует некоторый линейный оператор A. Поскольку векторы 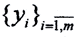линейно независимы, то коэффициенты при векторе y_k в левой и правой частях последней формулы должны совпадать, то есть 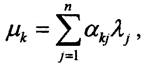или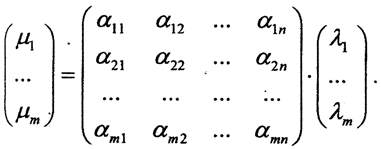

Определение 2. Оператор А ограничен, если для любых x ∈X, справедлива оценка ||Ax||≤c*||x||, где с - постоянная. Точная нижняя грань всех таких констант с называется нормой оператора А и обозначается ||A||. Другими словами, ||A|| = inf c.

Комментарий. По определению нормы, ∀x∈X ||Ax||≤||A||*||x||, то есть норма ||A||, во первых, одна из верхних граней, а во вторых ∀ε>0 ∃x_ε∈X:||Ax_ε||>(||A||-ε)*||x_ε||, что означает несдвигаемость верхней грани.

Теорема 1.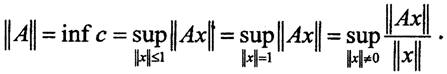

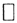
Обозначим 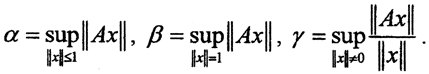Покажем, что 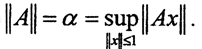Так как ||x||≤1, то ∀x:||x||≤1 ||Ax||≤||A||*||x||≤||A||. Тогда 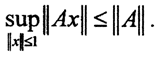С другой стороны, из несдвигаемости верхней грани следует, что ∀ε>0 ∃x_ε∈X:||Ax_ε||>(||A||-ε)-||x_ε||. Рассмотрим элемент 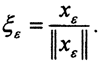Тогда для него 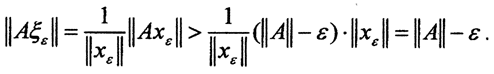Но норма ||ξ_ε|| = 1, поэтому 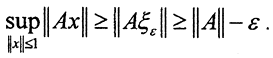В силу произвольности ε, сразу получаем 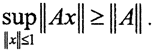Таким образом, 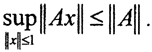Но одновременно 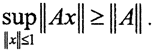, то есть 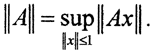Покажем теперь, что выполняются и остальные равенства. Для этого докажем, что α≥β≥γ≥α. Первое неравенство α≥β очевидно, поскольку в обеих его частях супремум берется от одной и той же величины ||Ax||. Второе неравенство β≥γ следует из того, что для любого ||x||≠0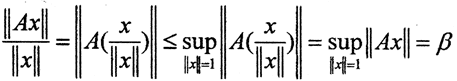 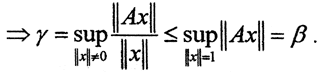Третье неравенство γ≥α следует из того, что для любого ||x||≠0 и ||x||≤1 имеем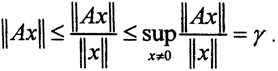

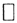
(Комментарий. Для числовых функций линейная функция всегда ограничена. В конечномерных пространствах любой линейный оператор является ограниченным. Для линейного оператора в бесконечномерных пространствах это, вообще говоря, не так.)

Пример 3. Оператор дифференцирования. Пусть оператор дифференцирования D действует из C[0,1] в C[0,1], то есть оператор Dx(t) = x'(t). Этот оператор определен не на всем пространстве непрерывных функций, а лишь на подпространстве непрерывных функций, имеющих непрерывную производную. В пространстве Cp0,1] норма 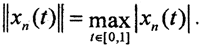Достаточно указать один элемент пространства, для которого ограниченность не имеет места. Возьмем из C[0,1] последовательность x_n(t) = tⁿ. Она ограничена в C[0,1], так как 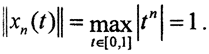Рассмотрим Dx_n(t) = x_n'(t) = nt^n-1 Тогда норма 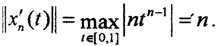Таким образом, оператор D переводит ограниченное множество в неограниченное, то есть этот оператор не является ограниченным. 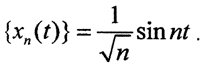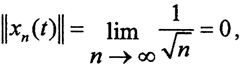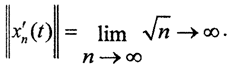Такая же ситуация с последовательностью В C[a,b] норма а Тогда 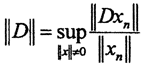при n→∞ тоже стремится к бесконечности, то есть оператор дифференцирования А неограничен, то есть не является непрерывным. Но если в пространстве исходных данных Х выбрать более сильную норму, то ситуация изменится. Рассмотрим пространство Х как пространство C¹[a,b] ⊂ C[a,b] а пространство У как пространство С[a,b]. Тогда 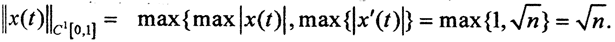Теперь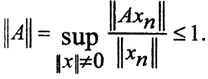

Пример. Линейный функционал в пространствах R²_∞, R²₁, R²₂ в точках (1,2) и (3,4) равен числам 5 и 6 соответственно. Найти его значение в точке (7,8) и норму.

Указание. Линейный функционал, заданный на плоскости, имеет вид f = ax+by, то есть это плоскость, проходящая через начало координат. Максимум этой функции на единичных шарах в соответствующих пространствах и будет нормой. Её можно найти, как условный экстремум функции f(t), где условиями будут уравнения соответствующих единичных шаров. Для пространств R²_∞, R²₁ легко сообразить, что максимум возможен только на стыках соответствующих отрезков, описывающих единичные шары. Для пространства R²₂ можно воспользоваться гармоническим преобразованием.

Пример. Значение линейного функционала в R²₂ в точке (1,1) равно -1, а его норма равна 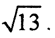Найти его значение в точке (7,8).

Линейный функционал, заданный на плоскости, имеет вид f = ax+by, то есть это плоскость, проходящая через начало координат. Его норма - это максимальное значение этой функции на единичном шаре в R²₂. Таким образом, имеем симметрическую СЛАУ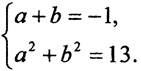

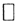
Эту задачу можно решить с помощью теоремы Рисса, которую мы рассмотрим позже.

Пример. Значение линейного функционала в R²_∞, R²₁ в точке (1,1) равно -1, а его норма равна 12. Найти его значение в точке (7,8).

(Комментарий. Из геометрического смысла понятия нормы видно, что общий вид линейного функционала в пространствах Rⁿ_∞, Rⁿ₁, Rⁿ₂ задаётся формулой 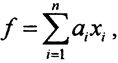где &38704;a_i∈R. Нормы же их определяются выражениями )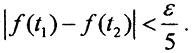

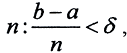
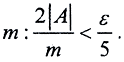Пример. Рассмотрим преобразование двумерного пространства X в двумерное пространство Y оператором A, причём матрица линейного оператора A невырождена и имеет вид 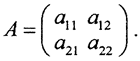У такого оператора можно посчитать конечное значение норм входного и выходного элементов, максимальное значение этого отношения на всем множестве определения дает согласованную норму самого этого оператора. Грубо говоря, это максимальный "коэффициент усиления" преобразования.

1. Рассмотрим преобразование R²₂→R²₂, где точки M₁(x₁,x₂), M₂(x˜₁,x˜₂)∈X а точки N₁(y₁,y₂), N₁(y˜₁,y˜₂)∈Y. Тогда y₁ = a₁₁x₁+a₁₂x₂, а y₂ = a₂₁x₁+a₂₂x₂. Обозначим Δx₁ = x₁ - x˜₁, Δx₂ = x₂ - x˜₂. Тогда ρ²(N₁,N₂) = (a₁₁Δx₁+a₁₂Δx₂)²+(a₂₁Δx₁+a₂₂Δx₂)². Запишем это как скалярное произведение и воспользуемся неравенством Буняковского-Коши. 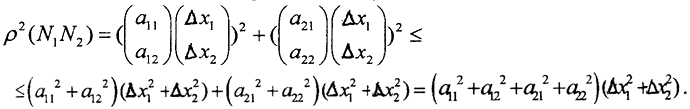Тогда ρ²(N₁,N₂)≤(a₁₁²+a₁₂²+a₂₁²+a₂₂²)^1/₂ ρ²(M₁,M₂), то есть 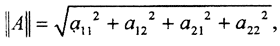а норма 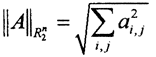называется эвклидовой.

2. Рассмотрим преобразование R²₁→R²₁.

ρ(N₁,N₂) = |y₁-y˜₁|+|y₂-y˜₂| = |Δy₁|+|Δy₂| = |a₁₁Δx₁+a₁₂Δx₂|+|a₂₁Δx₂+a₂₂Δx₂|≤(|a₁₁|+|a₂₁|)Δx₁+(|a₁₂|+|a₂₂|)Δx₂≤max {|a₁₁|+|a₂₁|,|a₁₂|+|a₂₂|}ρ(M₁,M₂). Тогда ||A||₁ = max {|a₁₁|+|a₂₁|,|a₁₂|+|a₂₂|}. Такая норма называется столбиковой.

3. Рассмотрим преобразование R²_∞→R²_∞.

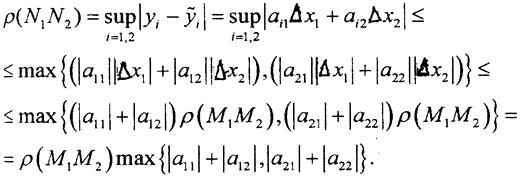
Тогда ||A||_∞ = max {|a₁₁|+||a₁₂|,||a₂₁|+|a₂₂|}. Такая норма называется строчной.