2.8. Топологический аспект понятия компактности

Определение 1. Открытым покрытием множества M⊂X называют конечную или бесконечную совокупность открытых множеств 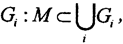причём ∀x∈M эта точка принадлежит хоть одному из множеств G_i.

Теорема 5 (Критерий компактности Гейне-Бореля). Множество K⊂X - компакт, если и только если из любого открытого покрытия {G_i} множества K можно выделить конечное подпокрытие G.

(Комментарий. В полном метрическом пространстве компакт - это замкнутое, вполне ограниченное множество. Пусть 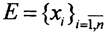конечная ε-сеть, то есть ∀ε>0 весь компакт K целиком разместится в объединении шаров B(x_i,ε), и если, в свою очередь, каждый такой шар целиком входит в некоторое множество G_i, то компакт 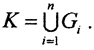Таким образом, нужно показать, что ∀ε>0 и ∀x∈K ∃B(x,ε):B(x,ε)⊂G_i.)

Необходимость.

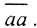
Пусть не существует шара, целиком входящего в некоторое множество G_i. Тогда ∃{ε_i}→0 и ∃{x_i}∈K, такие, что все шары B(x_i,ε_i)не попадут целиком ни в одно множество G_i. Но множество компакт, то есть из последовательности {x_i} можно выделить подпоследовательность {x_ik}→x₀. Эта точка x₀ принадлежит одному из открытых множеств G_i, то есть, по определению открытых множеств, она входит в множество G_i вместе с некоторой окрестностью. Стало быть, существует шар B(x₀,δ)⊂G_i, целиком входящий в множество G_i.

Достаточность.

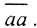
Пусть существует конечное покрытие множества K⊂X, но множество K - не компакт. Это означает, что никакая точка множества не может быть пределом последовательности или подпоследовательности, сходящейся к этой точке. Это означает, что у множества K вообще нет предельных точек, то есть все его точки изолированные. Другими словами, существует шар B(x,ε), внутри которого нет ни одной точки из множества K, кроме, быть может, точки x. Рассмотрим открытое покрытие множества K⊂X этими шарами. По условию, существует конечное покрытие множества K, то есть существует конечная совокупность шаров, которая покрывает бесконечное множество элементов множества K, но в каждом из этих шаров находится только по одной точке из множества K. То есть множество K конечно.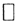

Определение 2. Множество K⊂X называется компактом, если из любого открытого покрытия {G_i} множества K можно выделить конечное подпокрытие G.

(Комментарий. Это определение позволило П.С. Александрову и П.С. Урысону построить теорию компактных топологических пространств, где компактность часто называют бикомпактностью. Та компактность, которой мы пользовались, называется секвенциальной компактностью (sequential (лат.) последовательность). Эти понятия, вообще говоря, различны и совпадают только в метрических пространствах.)

Теорема 2 (О структуре компакта). Любой компакт K гомеоморфен канторову дисконтинууму K_D.

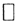
Покажем, что существует непрерывная функция φ, осуществляющая биекцию между компактом K канторовым дисконтинуумом K_D. Так как K - компакт, то ∀ε>0 для него существует конечная ε-сеть. Возьмём последовательность {ε_n} и построим её для каждого n. При n = 1 это будет {x₁₁,x₁₂,x₁₃,...,x_1m}, при n = n это будет {x_n1,x_n2,x_n3,...,x_nm}. При этом в каждую из них добавляем точки так, чтобы общее число точек в любой ε-сети было степенью двойки, то есть m_n = 2^k_n. Рассмотрим ε₁-сеть. Очевидно, что любое x∈K находится в одном из шаров с радиусом ε₁ и центрами в точках {x₁₁,x₁₂,x₁₃,...,x_1m}. Пусть, например, эта точка находится в шаре B(x_1k,ε₁), тогда при n = 2 эта точка находится в шаре B(x_2k,ε₂), и так далее. Таким образом, для любого x∈K можно указать бесконечную последовательность вложенных шаров с радиусами ε_n→0, внутри которых она находится. Общее число таких шаров, образующих ε-сеть, конечно и является степенью двойки.

Рассмотрим теперь построение канторова дисконтинуума K_D[0,1]. На k-м шаге он содержит 2^k сегментов ранга k. Если их как-то пронумеровать, например, слева направо в порядке следования сегментов, то ∀t∈K_D[0,1] ∃! последовательность вложенных друг в друга сегментов, содержащих эту точку. Тогда ей можно сопоставить точку x∈K и последовательность вложенных шаров с теми же номерами, внутри которых она находится. Это биективное соответствие осуществляется функцией x = f(t). Покажем, что она непрерывна. Для произвольного ε>0 рассмотрим шар B(x₀,ε), где x₀ = f(t₀). Рассмотрим последовательность {ε_n} вложенных шаров с радиусами ε_n→0, Так как ε_n→0, то ясно, что, начиная с некоторого N, шары B(x₀,ε_n) окажутся внутри любого шара B(x₀,ε) с фиксированным ε>0. Если в качестве δ взять наименьшее расстояние от t₀ до конца сегмента, содержащего на N-м шаге точку t₀, то как только |t-t₀|<δ, сразу |x-x₀| = |f(t)-f(t₀)|<ε, то есть функция x = f(t) непрерывна.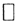

(Комментарий. Непрерывные на компакте функционалы ведут себя так же, как и функции, непрерывные на сегменте, то есть для них имеет место теорема Вейерштрасса.)

Теорема 3 (Теорема Вейерштрасса). Непрерывный на компакте K⊂X функционал f(x)

2) достигает на нём своих точных верхней и нижней граней.

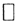
1. Пусть функционал f(x) не ограничен на компакте K⊂X, то есть ∀n∈N∃ точка x_n⊂K:|f(x_n)|>n. Так как K⊂X компакт, выделим из последовательности x_n подпоследовательность x_nk→x₀⊂K. Но функционал f(x) непрерывен, то есть f(x_nk)→f(x₀), а по условию |f(x_nk)|>n_k, следовательно, исходная посылка неверна.

2. Так как функционал f(x) непрерывен на компакте K⊂X, он ограничен на нём, то есть множество его значений ограничено, то есть он имеет точную верхнюю грань M и точную нижнюю грань m. Надо показать, что функционал f(x) достигает их на компакте K. Покажем это для точной верхней грани M. По определению точной верхней грани M ∀ x∈K f(x)≤M и 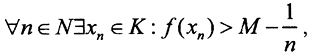то есть 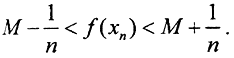Выделим из последовательности {x_n} подпоследовательность {x_nk}→x₀⊂K, то есть 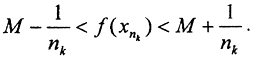При n→∞ по теореме о двух милиционерах 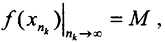а силу непрерывности f(x₀) = M, и, так как K - компакт, x₀∈K.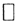

Пример. В конечномерном пространстве Rⁿ любое ограниченное множество M⊂Rⁿ предкомпактно.

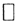
Рассмотрим замкнутое множество 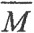, M⊂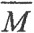 и произвольную последовательность в нём. По теореме Больцано-Вейерштрасса из неё можно выделить сходящуюся подпоследовательность, причём она будет сходиться к элементу из 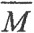, то есть 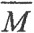- компакт, следовательно, M⊂ 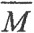- предкомпакт.

Пример. В пространстве C[0,1] множество M = {x_n(t)} = tⁿ не предкомпактно.

Если это множество предкомпактно, то из него можно выделить сходящуюся подпоследовательность {x_nk(t)} = t^n_k, которая по теореме Кантора должна сходиться равномерно, но равномерная сходимость влечёт поточечную, то есть сходимость в каждой точке пространства C[0,1].

Однако, подпоследовательность {x_nk(t)} = t^n_k при t∈[0,1) сходится к нулю, а при t = 1 к единице, то есть к разрывной функции, не принадлежащей пространству C[0,1]. v

Определение 3. Множество функций F⊂C[a,b] равномерно ограничено, если ∃A>0: ∀x(t)∈F, ∀t∈[a,b]|x(t)|≤A.

Определение 4. Множество функций F⊂C[a,b] равностепенно непрерывно, если ∀t₁,t₂∈[a,b] и ∀x(t)∈F: ∀ε>0 ∃δ=δ(ε):(|t₁-t₂|<δ ⇒|x(t₁)-x(t₂)|<ε).

Пример. Рассмотрим в пространстве C[0,1] последовательность {y_n} = Asin2ⁿπx. Эта последовательность, очевидно, равномерно ограничена в C[0,1]. Однако, как показано ранее, она не равностепенно непрерывна, точно так же, как и последовательность {y_n} = {sin nx} в пространстве C[0,1]. Эта последовательность равномерно ограничена, так как 0≤|sin nt|≤1 ∀t∈[0,π], но не равностепенно непрерывна. Пусть 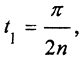t₂ = 0. Тогда 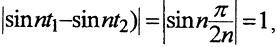что и означает невыполнение условия равностепенной непрерывности.

Теорема 4 (Критерий компактности Арцела Асколи). Множество функций F⊂C[a,b] компактно, если и только если оно равномерно ограничено и равностепенно непрерывно.

Необходимость.

Пусть множество F компактно в C[a,b].

1. Докажем, что оно равномерно ограничено. Так как пространство C[a,b] полное, а множество F компактно, то существует конечная ε-сеть из функций {x₁(t), x₂(t), ..., x_n(t)}. Каждая из них ограничена (как непрерывная функция на компакте), а для произвольной функции x(t)∈F найдётся x_k(t) из ε-сети такая, что ρ(x,x_k)<ε. Тогда 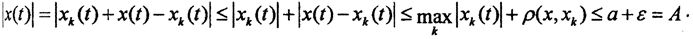. Это и означает равномерную ограниченность множества F функций x(t)∈F.

2. Докажем равностепенную непрерывность множества F. Так как множество F компактно, то ∀ε>0 существует конечная 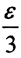-сеть, состоящая из функций E = {x₁(t), x₂(t), ..., x_n(t)}, таких, что 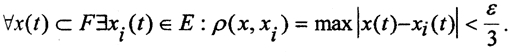Так как все функции x_k(t) непрерывны на компакте F, то по теореме Кантора они и равномерно непрерывны на нём, т.е. ∀t₁,t₂∈[a,b] ∀ε>0 ∃δ=δ(ε):(|t₁-t₂|<δ_i⇒|x_i(t₁)-x_i(t₂)|<ε). Пусть δ = min (δ₁, δ₂,...,δ_m). Тогда это наименьшее значение подойдёт для любых функций x_k(t) из сети. Покажем, что это значение подойдёт и для любой функции x(t)∈F. Пусть x(t)∈F - произвольная функция множества F, а функция x_k(t) из 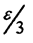-сети. Тогда имеем 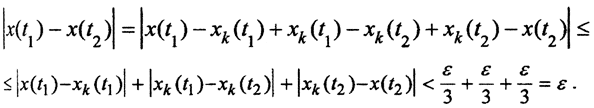Итак, |x(t₁)-x(t₂)|<ε, что и означает равностепенную непрерывность.

Достаточность.

Пусть F - равномерно ограниченное и равностепенно непрерывное на семейство функций f(t). Покажем, что семейство F - компакт, то есть ∀ε>0 построим конечную ε-сеть.

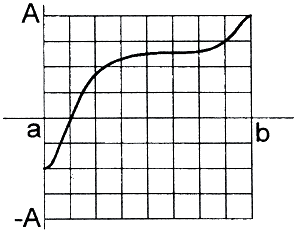
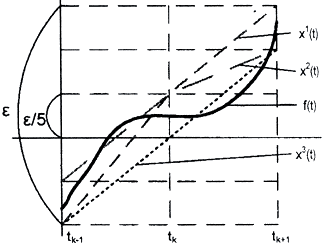
Пусть все функции f(t) ограничены, то есть ∀f(t) |f(t)|≤A. Зафиксируем сколь угодно малое ε>0. Так как все функции f(x) равностепенно непрерывны, то ∃δ=δ(ε):∀f(t)∈F и ∀t₁, t₂∈[a,b] как только |t₁-t₂|<δ, сразу 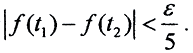Разобьём сегмент [a,b] точками {t₀ = a, t₁, t₂, ..., t_n = b}, причём 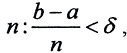а сегмент {-A,A] разобьём точками {y₀ = -A, y₁, y₂, ..., y_m = A}, причём 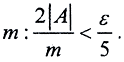Сопоставим каждой функции f(t) ломаную x(t) с вершинами в узлах сетки, причём так, что ∀t_k значение x(t_k) берётся такое, что 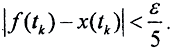Очевидно, это всегда возможно. Таким образом, 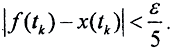, 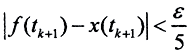и 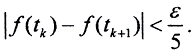Тогда 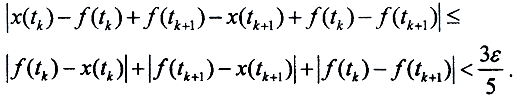То есть 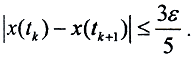Так как между точками t_k и t_k+1 функция x(t) линейна, то и 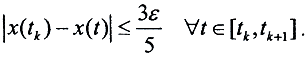Пусть теперь t - произвольная точка из сегмента [a,b], а t_k - ближайшая к ней слева. Тогда |f(t)-x(t)| = |f(t)-f(t_k)+f(t_k)-x(t_k)+x(t_k)-x(t)|≤|f(t)-f(t_k)|+|f(t_k)-x(t_k)|+|x(t_k)-x(t)|≤ε. Таким образом, ломаные x(t) и в самом деле образуют конечную сеть по отношению к множеству функций f(t)∈F.

Пример. Является ли множество 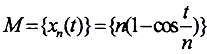предкомпактным в пространстве C[0,1]?

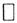
Это множество равномерно ограничено, так как 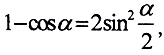а sinα≤α. Тогда 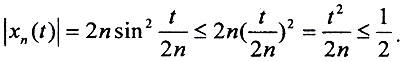Кроме того, оно равностепенно непрерывно, так как по формуле конечных приращений Лагранжа 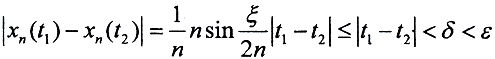при |t₁-t₂|<δ<ε сразу для всех n. Тем самым, множество 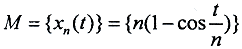предкомпактно в пространстве C[0,1].