
2.6. Конструкция интеграла Лебега
Пусть D⊂Rn⊂X - измеримое множество, на котором задана ограниченная и измеримая функция (функционал) y=f(x).
1. Обозначим 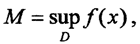 , а
, а 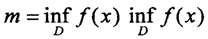 и назовём δyn - разбиением произвольное множество точек m=y0<y1<y2<...<yn=M.
и назовём δyn - разбиением произвольное множество точек m=y0<y1<y2<...<yn=M.
2. Пусть Δyi=yi-yi-1, а 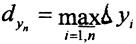 - диаметр разбиения при фиксированном n. При изменении n или при выборе других точек разбиения диаметр разбиения будет меняться. δyn - разбиение называется нормальным, если
- диаметр разбиения при фиксированном n. При изменении n или при выборе других точек разбиения диаметр разбиения будет меняться. δyn - разбиение называется нормальным, если 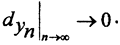
3. Лебеговым разбиением множества D⊂Rn⊂X называется кортеж {Dk}, где 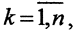 а D=∪Dk, Di∩Dj, если i≠j. Здесь
а D=∪Dk, Di∩Dj, если i≠j. Здесь 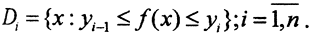
4. Пусть ξk∈Dk - произвольная точка элемента кортежа {Dk}. Составим сумму 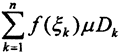 - интегральную сумму Лебега.
- интегральную сумму Лебега.
5. Число 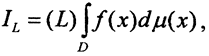 если оно существует, называется определённым интегралом Лебега от ограниченной и измеримой функции y=f(x), заданной на измеримом множестве D, если для любой нормальной последовательности δyn- разбиений, любого выбора точек ξk и ∀ ε>0∃ N=N(ε) и δ=δ(ε):∀n>N и
если оно существует, называется определённым интегралом Лебега от ограниченной и измеримой функции y=f(x), заданной на измеримом множестве D, если для любой нормальной последовательности δyn- разбиений, любого выбора точек ξk и ∀ ε>0∃ N=N(ε) и δ=δ(ε):∀n>N и 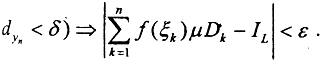
(Комментарий. Определение интеграла Лебега аналогично определению интеграла Римана, но только интегральные суммы составляются разбиением не области определения, а множества значений функции. Если у вас есть несколько конвертов с деньгами, то пересчитать их можно или посчитав деньги в каждом конверте (метод Римана), или выложив их из конвертов и сгруппировав по купюрам (метод Лебега). Отсюда ясно, что функция, интегрируемая по Риману, будет интегрироваться и по Лебегу, и интегралы будут совпадать. Обратное, вообще говоря, неверно. Для существования интеграла Римана необходимо и достаточно (теорема Дюбуа-Раймона), чтобы множество точек конечного разрыва имело меру ноль. По Лебегу можно интегрировать и всюду разрывные функции. Например, функция Дирихле разрывна во всех иррациональных точках, то есть множество точек разрыва имеет меру один. Она не интегрируема по Риману, но интегрируема по Лебегу: I=1*μ(Q)+0*μ(Ir)=0. Для интеграла Лебега имеют место свойства, совпадающие с соответствующими свойствами интеграла Римана с точностью до формулировок.)
Примеры.
1. Взять интеграл Лебега 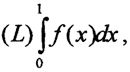 если
если 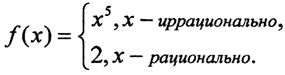

На сегменте [0,1] множество рациональных чисел имеет меру ноль. Тогда функция интегрируема по Риману и 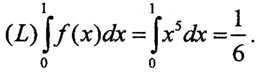

2. Вычислить с точностью до 0,001 интеграл Лебега от функции f(x)=2xна множестве M, полученном удалением из отрезка [0,1] интервалов 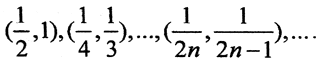

Это множество есть объединение множества меры ноль, состоящего из точек 0 и 1, и сегментов 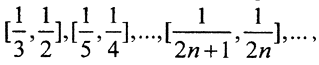 на каждом из которых функция интегрируема по Риману:
на каждом из которых функция интегрируема по Риману: 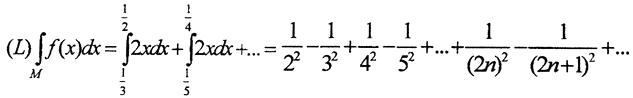

|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'