
2.5. Схема построения интеграла Лебега (На множестве конечной меры)
1. Разбиение области интегрирования осуществляется по признаку близости значений интегрируемой функции.
2. Рассматриваются простые измеримые функции y=f(x), то есть функции, принимающие не более чем счетное число значений {y1,y2,y3,...}, где yi≠ yj при i≠ j. Для таких функций под интегралом по множеству D⊂ X понимается сумма или ряд (при условии абсолютной сходимости) 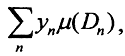 где μ(Dn) - меры тех отрезков, на которых функция y=f(x) принимает значения yn. То есть
где μ(Dn) - меры тех отрезков, на которых функция y=f(x) принимает значения yn. То есть 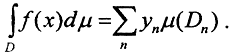
3. Множество значений простых функций, можно рассматривать, как метрическое пространство с метрикой 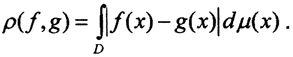 Но значений не более чем счётное число, то есть это множество первой категории, следовательно, пространство Y значений yn не полное. Пополнение этого пространства осуществляется по схеме доказательства теоремы Хаусдорфа о пополнении метрического пространства.
Но значений не более чем счётное число, то есть это множество первой категории, следовательно, пространство Y значений yn не полное. Пополнение этого пространства осуществляется по схеме доказательства теоремы Хаусдорфа о пополнении метрического пространства.
4. Из элементов данного неполного метрического пространства строится полное пространство, где в качестве классов эквивалентности, объявляется множество всех почти всюду равных простых измеримых функций, почти всюду (или равномерно) сходящихся к функции y=f(x). Таким образом, мы получили новое фактор - множество Y, элементами которого являются непересекающиеся классы фундаментальных последовательностей {αn}, {βn}, {γn},..., представителями которых являются фундаментальные последовательности {xn}, {yn}, {zn},... пространства (Y,ρ). Если фундаментальная последовательность {xn} сходится к точке y, то и эквивалентная ей последовательность {αn} сходится к той же точке. Сходимость 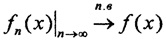 влечёт за собой существование предела
влечёт за собой существование предела 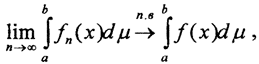 который и объявляется интегралом Лебега
который и объявляется интегралом Лебега 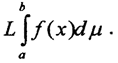
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'