
2.4. Понятие измеримой функции
Определение 1. Если какое - либо утверждение верно для любой точки множества M (за исключением, быть может, множества точек, имеющих меру ноль), то говорят, что это утверждение верно почти всюду.
Определение 2. Две функции x1(t) и x2(t), заданные на одном и том же множестве X, называются эквивалентными x1(t) x2(t), или
x2(t), или 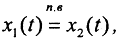 если mes{t:x1(t)≠x2(t) = 0.
если mes{t:x1(t)≠x2(t) = 0.
Пример 1. Функция Дирихле 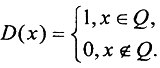 Так как множество рациональных чисел имеет меру ноль, то D(x)
Так как множество рациональных чисел имеет меру ноль, то D(x) 0 или
0 или 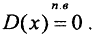
Определение 3. Пусть X - некоторое множество, P(X) - множество всех подмножеств множества X, а R⊂P(X) - σ-алгебра. Вещественная функция f(x):x∈X называется измеримой, если при любом конечном a∈R множество Xa(x:f(x)>a) (то есть множество тех x∈X, для которых f(x)>a), принадлежит σ-алгебре R, то есть измеримо.
Пример 2. Пусть f(x)=x2, x∈[0,1]. Тогда Xa=[0,1], a∈0, a∈[0,1)⇒Xa=[a,1], Xa=∅, a≥1.
Примем без доказательств некоторые факты:
1. Всякая функция, заданная на множестве меры нуль, измерима.
2. Вместо множества Da(f>a) можно взять множества Da(f≥a), Da(f<a), Da(f≤a).
3. Пусть функция f(x):x∈D⊂X измерима, а A⊂D измеримое подмножество D. Тогда функция f(x), рассматриваемая только для x∈A измерима.
4. Если f(x):x∈D⊂X измеримая функция, а g(x)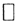 f(x), то g(x) также измерима.
f(x), то g(x) также измерима.
5. Пусть функции f(x) и g(x) - конечные измеримые функции, заданные на измеримом множестве D⊂X. Тогда 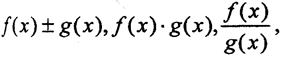 измеримы.
измеримы.
6. Пусть функция f(x) измерима на множествах D1,D2,...,Di,.... Тогда она измерима на их объединении 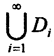 и пересечении
и пересечении 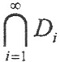 .
.
7. Критерий Лузина измеримости функций. Функция f(x) измерима на сегменте [a,b] если и только если ∀ε>0 ∃ g(x), непрерывная на сегменте [a,b], такая, что μ{x∈[a,b]:f(x)≠g(x)}≤ε.
(Комментарий. Критерий Лузина означает, что измеримые функции близки к непрерывным в том смысле, что любую из них можно сделать непрерывной, изменив её значения на множестве сколь угодно малой меры. Например, скачок 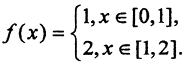 )
)
Пример 3. Функция Дирихле, определённая, например, на отрезке [0,1], измерима, так как при а<0 ⇒Xa=[0,1], a при a∈[0,1)⇒Xa=[a,1], но так как множество рациональных чисел имеет меру ноль, то в обоих случаях 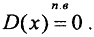 Если, a≥1⇒Xa = ∅, а пустое множество имеет меру ноль.
Если, a≥1⇒Xa = ∅, а пустое множество имеет меру ноль.
Определение 4. Пусть на измеримом множестве X задана последовательность измеримых и почти везде конечных функций {fn(x)} = {f1(x), f2(x), f3(x),...} и измеримая и почти везде конечная функция f(x). Если ∀ε>0 верно, что 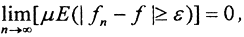 то говорят, что последовательность функций сходится к функции f(x) по мере
то говорят, что последовательность функций сходится к функции f(x) по мере 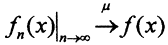 или fn(x)⇒f(x)(обозначение Фихтенгольца).
или fn(x)⇒f(x)(обозначение Фихтенгольца).
Определение 5. Пусть на измеримом множестве задана последовательность измеримых и почти везде конечных функций {fn(x)} = {f1(x), f2(x), f3(x),...} и измеримая и почти везде конечная функция f(x). Если последовательность {fn(x)} сходится к функции f(x), за исключением, быть может, множества точек, имеющих меру ноль, то говорят, что последовательность функций сходится к функции f(x) почти всюду 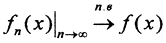 или fn(x) →f(x). Это так называемая поточечная сходимость.
или fn(x) →f(x). Это так называемая поточечная сходимость.
Определение 6. Равномерная сходимость на множестве X означает, что 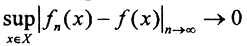 и обозначается
и обозначается 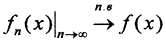 или
или 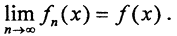
(Комментарий. Ясно, что из равномерной сходимости следует сходимость почти всюду, потому, что равномерная сходимость - это "сходимость всюду". Обратное, вообще говоря, неверно. Однако имеет место)
8. Теорема Егорова о сходимости почти всюду. Если 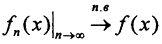 на множестве X конечной меры, то ∀ε>0 ∃Xε⊂X:mesXε<ε и
на множестве X конечной меры, то ∀ε>0 ∃Xε⊂X:mesXε<ε и 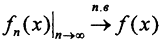 вне подмножества Xε.
вне подмножества Xε.
9. Теорема Лебега о сходимости почти всюду. Если 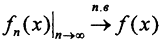 то
то 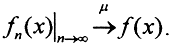
(Комментарий. Обратное, вообще говоря, неверно. Однако, имеет место)
10. Теорема Лебега о сходимости по мере. Из любой последовательности, такой, что 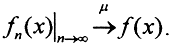 можно выделить подпоследовательность {fnk(x)}, такую, что
можно выделить подпоследовательность {fnk(x)}, такую, что 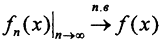 .
.
(Комментарий. Итак, равномерная сходимость влечет сходимость почти всюду, а сходимость почти всюду влечет (на множестве конечной меры) сходимость по мере. Обратные утверждения неверны.)
Пример 4. Рассмотрим функциональную последовательность, заданную на отрезке x∈[0,1]. 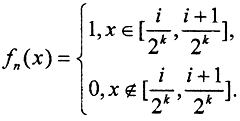 Здесь
Здесь 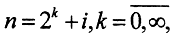 i∈[0,2k). Построим несколько членов этой функциональной последовательности: n=1 ⇒k=0, i=0,⇒f1(x)=1 ∀x∈[0,1];. При k=1, i={0,1}. При этом n={2,3}, f2(x)=1 при
i∈[0,2k). Построим несколько членов этой функциональной последовательности: n=1 ⇒k=0, i=0,⇒f1(x)=1 ∀x∈[0,1];. При k=1, i={0,1}. При этом n={2,3}, f2(x)=1 при 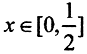 и f3(x)=1 при
и f3(x)=1 при 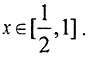 При k=2 i={0,1,2,3}. При этом n={4,5,6,7}, а fn(x)=1 последовательно на всех четвертушках отрезка x∈[0,1]. Ясно, что имеет место сходимость по мере, то есть fn(x)⇒f(x)≡0, так как
При k=2 i={0,1,2,3}. При этом n={4,5,6,7}, а fn(x)=1 последовательно на всех четвертушках отрезка x∈[0,1]. Ясно, что имеет место сходимость по мере, то есть fn(x)⇒f(x)≡0, так как 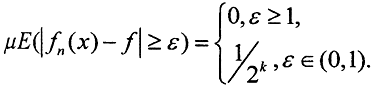 Но здесь нет сходимости почти всюду, так как последовательность fn(x) не сходится ни в одной точке отрезка [0,1], то есть на множестве положительной меры. Выделим из неё подпоследовательность fnk(x)={f1,f2,f4,f8,f16,...}. Ясно, что fnk(x)→0 удалённых ин; почти всюду, кроме точки x=0.
Но здесь нет сходимости почти всюду, так как последовательность fn(x) не сходится ни в одной точке отрезка [0,1], то есть на множестве положительной меры. Выделим из неё подпоследовательность fnk(x)={f1,f2,f4,f8,f16,...}. Ясно, что fnk(x)→0 удалённых ин; почти всюду, кроме точки x=0.
Пример 5. Из сходимости почти всюду не следует сходимость в среднем. Рассмотрим функциональную последовательность 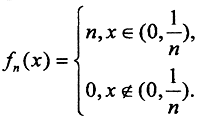 Последовательность {Xn} множеств, на которых функциональная последовательность fn(x) равна нулю
Последовательность {Xn} множеств, на которых функциональная последовательность fn(x) равна нулю 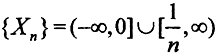 монотонно возрастает и стремится ко всей прямой, за исключением точки ноль, то есть множества меры ноль. Это и есть, по определению, сходимость почти всюду. Однако в среднем эта функциональная последовательность к нулю не сходится, так как
монотонно возрастает и стремится ко всей прямой, за исключением точки ноль, то есть множества меры ноль. Это и есть, по определению, сходимость почти всюду. Однако в среднем эта функциональная последовательность к нулю не сходится, так как 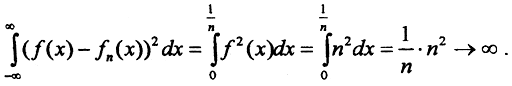 .
.
Пример 6. Из сходимости в среднем не следует сходимость почти всюду.
Рассмотрим функциональную последовательность, заданную на отрезке x∈[0,1] таким образом: 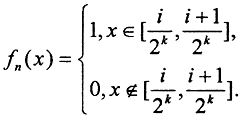 Здесь
Здесь 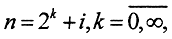 i∈[0,2k). Здесь нет сходимости почти всюду, так как последовательность fn(x) не сходится ни в одной точке отрезка [0,1]. Однако в среднем последовательность fn(x) сходится к нулю, так как при f(x) = 0 можно записать, что
i∈[0,2k). Здесь нет сходимости почти всюду, так как последовательность fn(x) не сходится ни в одной точке отрезка [0,1]. Однако в среднем последовательность fn(x) сходится к нулю, так как при f(x) = 0 можно записать, что 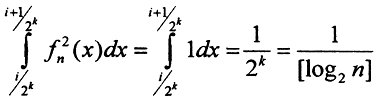 и стремится к нулю при n→∑, то есть
и стремится к нулю при n→∑, то есть 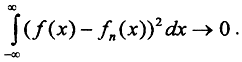
Пример 7. Из сходимости по мере не следует сходимость в среднем. Рассмотрим функциональную последовательность, заданную на отрезке x∈[0,1]: 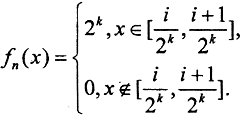 . Здесь
. Здесь 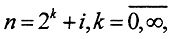 i∈[0,2k). Как и в примере 4, здесь имеет место сходимость по мере, то есть fn(x)⇒f(x)≡0, так как
i∈[0,2k). Как и в примере 4, здесь имеет место сходимость по мере, то есть fn(x)⇒f(x)≡0, так как 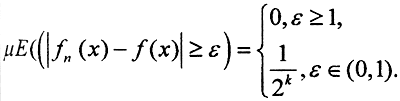 Тем не менее сходимости в среднем нет, так как
Тем не менее сходимости в среднем нет, так как 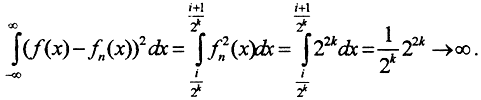
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'