2.3. Понятие меры Лебега

Пусть множество A⊂R² - ограниченная плоская фигура, которую без ограничения общности можно считать целиком принадлежащей квадрату [0,1]*[0,1] на плоскости. Алгоритм введения меры Лебега выглядит таким образом:

1. По определению будем считать, что мера прямоугольника P, mesP=a*b. Назовём элементарным плоским множеством (ступенчатой фигурой) такое множество, которое можно представить в виде объединения конечного числа непересекающихся прямоугольников.

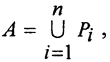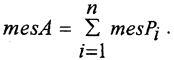2. Полагаем, что если множество то Для прямоугольников можно доказать, а для других элементарных множеств постулируется σ-аддитивность.

3. Покрытием множества A называется такая совокупность множеств G_α⊂X, что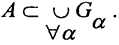

4. Внешняя мера μ^* определяется так: 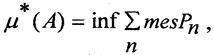где инфинум берётся по всем возможным покрытиям множества конечной или счётной совокупностью прямоугольников P_n или других элементарных множеств.

5. Определим некоторое множество A_ε как объединение конечного числа непересекающихся прямоугольников или других элементарных множеств. Это измеримое элементарное множество.

6. Множество A измеримо по Лебегу, если 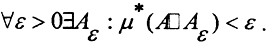Здесь 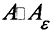- дизъюнктивная сумма множеств A и A_ε. Внешняя мера μ^*, определённая только на измеримых множествах, называется мерой Лебега множества A.

Теорема 4 (Теорема Лебега о σ-аддитивности меры). Пусть Ω_h - попарно непересекающаяся совокупность измеримых множеств, то есть Ω_i∩Ω_j=∅ если i≠j и 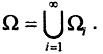Тогда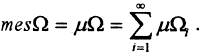

(Комментарий. Стало быть, совокупность измеримых множеств замкнута относительно операции счётного объединения, а мера σ-аддитивна.)

Теорема 5 (О непрерывности σ-аддитивной меры). Если

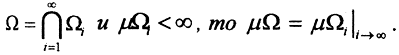
Без доказательства.

(Комментарий.

3. При построении меры по Жордану множество A "зажималось" системой прямоугольников, Q=Q_n - внутренних и P=P_n - внешних, и если 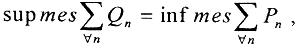то множество измеримо. Определив функцию ρ = mes(P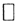Q), мы получим полуметрику, так как разные системы прямоугольников могут покрывать одну и ту же фигуру. Это значит, что ρ = mes(P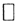Q) = 0 при разных P и Q. Если отождествить те P и Q, при которых ρ = mes(PQ) = 0, то это уже метрика. Фактор-множество по отношению эквивалентности mes(PQ) = 0 образует метрическое пространство. Но это неполное метрическое пространство. Его пополнение и приводит к мере Лебега.)

Определение 1. Множество A⊂Rⁿ₂ имеет лебегову меру ноль, если ∀ε>0, можно указать последовательность открытых параллелепипедов V_k, такую, что 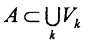и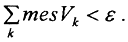

Пример 1. Меру ноль имеет любое дискретное множество, любое конечное или счётное множество, например, множество рациональных чисел (как объединение конечного или счётного числа точек, имеющих меру ноль).

Пронумеруем множество рациональных чисел 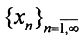и вокруг любого числа x_n рассмотрим интервал 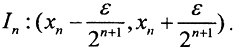Его мера (длин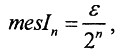а) а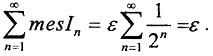

Переходя к дополнениям, получим, что мерой множества иррациональных чисел на отрезке будет длина отрезка.

Множество рациональных чисел стало измеримым, имеет лебегову меру ноль, но это всюду плотное множество первой категории. Может ли несчётное множество иметь меру ноль?

Пример 2. Покажем, что канторов дисконтинуум есть замкнутое, совершенное, нигде не плотное множество лебеговой меры ноль и мощности континуума.

1. Замкнутость. Канторов дисконтинуум K есть пересечение K_n замкнутых отрезков, оставшихся на n-м шаге процедуры с отрезком [0,1], то есть 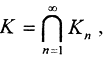а это замкнутое множество.

2. Совершенство. По процедуре, мы никогда не выбрасываем два смежных интервала, то есть в множестве K нет изолированных точек.

3. Нигде не плотность. Возьмём произвольный интервал (a,b)∈[0,1] и покажем, что ∃(α,β)∈(a,b)∈[0,1], не содержащий точек множества K. В самом деле: или на n-ном шаге процедуры интервал (a,b) уже не содержит точек множества K, или на следующем шаге мы выбрасываем из него треть, а это и есть тот самый интервал (α,β)∈(a,b), не содержащий точек множества K.

4. Мера ноль. Сумма длин выброшенных интервалов 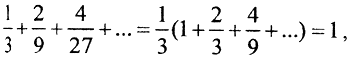то есть то, что осталось имеет меру ноль.

5. Мощность континуума. Процедура Кантора подразумевает деление соответствующего отрезка на каждом шаге на три равные части, то есть любое число x∈X есть троичная дробь, каждая цифра которой - 0, 1 или 2. Но множество K устроено так, что цифра запрещена, то есть это фактически двоичная дробь. Ранее была установлена биекция между точками отрезка [0,1] и действительными числами, записанными в любой системе счисления. А отрезок [0,1] имеет мощность континуума.

(Комментарий. Канторов дисконтинуум не имеет внутренних точек, так как если точка M внутренняя, то существует окрестность точки M, целиком принадлежащая множеству K, то есть U_M⊂K. Но тогда мера μU_M>0, и μK>0. Процедура Кантора позволяет строить на отрезке замкнутые, совершенные, нигде не плотные множества мощности континуума и произвольной лебеговой меры, меньшей, чем длина отрезка.)

Пример 3. Построим на отрезке [0,1] замкнутое, совершенное, нигде не плотное множество мощности континуума и с заданной мерой μ<1.

Удалим из отрезка [0,1] интервал E₁ длиной 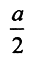с центром в середине отрезка. Далее из двух образовавшихся отрезков удалим по равному интервалу суммарной длиной 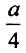с центрами в их серединах, и так далее. Объединение удалённых интервалов 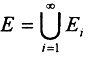- открытое множество, тогда множество D = [0,1]/E - множество замкнутое. Мера удалённого множества 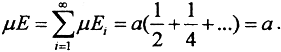Мера оставшегося множества μD = 1-a.