2.2. Понятие меры
Понятие меры есть естественное обобщение понятий длины, площади, объёма и их приложений.
Пример. Рассмотрим идущий от античности способ измерения площади - метод палеток. Пусть E⊂R2 - ограниченная плоская фигура, которую без ограничения общности можно считать целиком принадлежащей квадрату [0,1]*[0,1] на плоскости.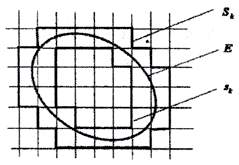 
Разобьем этот квадрат на k квадратов (палеток) и обозначим через sk(E) множество тех квадратов, которые целиком содержатся в множестве E, а через Sk(E) - множество тех квадратов, каждый из которых пересекается с E. Ясно, что sk(E)⊂E⊂Sk(E). Обозначим через μsk(E) и μSk(E) площади соответствующих множеств квадратов. Тогда при возрастании k множества sk(E) возрастают, а множества Sk(E) убывают, то есть
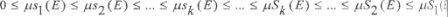
Последовательность {μsk(E)} не убывает и ограничена сверху, а последовательность {μSk(E)} не возрастает и ограничена снизу. Поэтому эти последовательности имеют пределы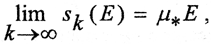 
и 
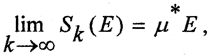которые называются соответственно внутренней и внешней мерой Жордана множества E. Если они совпадают, то есть 
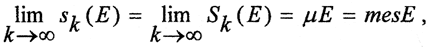то mesE называется мерой Жордана множества E, а фигура E называется измеримой (квадрируемой).
Аналогично строится мера Жордана для множества E⊂Rn и для множества E⊂R. Длина, площадь, объём обладают естественными свойствами, которые, как всегда, примем за аксиомы.
Определение 1. Под мерой будем понимать функцию, заданную на множестве всех измеримых фигур, обладающую следующими свойствами:
1. mesE≥0, mes∅=0.
2. Мера суммы конечной или счётной системы попарно непересекающихся множеств равна сумме их мер: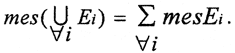
3. При перемещении множества как твёрдого тела его мера не меняется.
4. Мера единичного квадрата(отрезка, куба) равна единице.
(Комментарий. Пример измеримого, но очень специфического множества даёт канторов дисконтинуум. Это подмножество отрезка [0,1] числовой оси, состоящее из всех чисел вида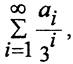 
где ai равно 0 или 2, которое получается следующим образом. Отрезок [0,1] делится на три части и затем выбрасывается средняя часть 
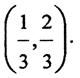Оставшиеся отрезки 
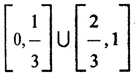вновь делим на три части и выбрасываем средние части 
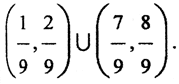И так далее. Это называют процедурой Кантора.
Ясно, что множество тех сегментов, которые целиком содержатся в канторовом дисконтинууме, пусто. Множество же тех сегментов, каждый из которых пересекается с отрезком [0,1] образует последовательность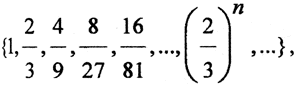 
которая стремится к нулю. Таким образом, мера Жордана канторова дисконтинуума равна нулю.
Не все множества измеримы по Жордану. Опять применим процедуру Кантора к отрезку [0,1] и удалим из него интервал с длиной, меньшей, чем 1/4. Затем из каждого из получившихся двух сегментов удалим интервалы с общей длиной, меньшей, чем 1/8, и так далее. В результате общая длина удалённых частей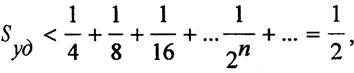 
то есть то, что осталось, имеет длину 
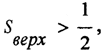тогда как фигура не содержит никакого отрезка. Это значит, что Sнижн. = 0. Стало быть, фигура неизмерима по Жордану.
Ещё один важный пример. Рассмотрим множество рациональных чисел сегмента [0,1]. Это множество плотно на сегменте [0,1]. То есть между любыми двумя точками сегмента [0,1] найдутся как рациональные числа, так и иррациональные. Разделим сегмент [0,1] на две части, затем на четыре части и т. д. Множество тех сегментов, которые целиком содержатся во множестве рациональных чисел, пусто, и его мера равна нулю. Множество же тех сегментов, каждый из которых пересекается с отрезком [0,1], просто состоит из этих сегментов, то есть их объединение и составляет отрезок [0,1], мера которого по определению равна единице. То есть множество рациональных чисел неизмеримо по Жордану. Абсолютно такие же рассуждения приводят к тому, что множество иррациональных чисел тоже неизмеримо по Жордану. Получается, что отрезок [0,1], мера которого равна единице, состоит из неизмеримых множеств.
Кроме того, мера Жордана не обладает счётной - аддитивностью (счётной аддитивностью). Это значит, что объединение счётного числа непересекающихся измеримых множеств может и не быть измеримым множеством. Например, точка измерима по Жордану и мера её ноль, но счётное множество точек множество рациональных чисел неизмеримо по Жордану. Следовательно, не выполняется свойство 2 определения меры. Таким образом, возникает задача расширения числа измеримых множеств.)
|
ПОИСК:
|
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'