II. Основные теоремы о пространствах

2.1. Полные метрические пространства

Теорема 1 (Критерий полноты Кантора). Метрическое пространство полно, если и только если любая последовательность непустых вложенных замкнутых шаров, радиусы которых стремятся к нулю, имеет непустое пересечение.

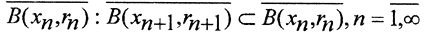Необходимость. Пусть последовательность вложенных шаров при r_{n →∞}→0 и пространство (X,ρ) полное. Тогда существует и единственна точка x₀, принадлежащая всем шарам сразу. Рассмотрим последовательность {x_n} центров этих шаров и оценим расстояние ρ(x_n,x_m) при m>n. Так как при 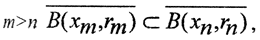, но по условию теоремы r_n→0, стало быть и ρ(x_n,x_m)→0 при n,m→∞. То есть последовательность {x_n} фундаментальна и в силу полноты пространства {X,ρ} сходится. Члены её, начиная с m-го, принадлежат шару 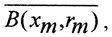так как шар замкнутый, то и предел 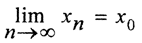принадлежит этому шару, а 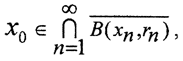то есть пересечение шаров не пусто.

Достаточность. Пусть {x_n} - произвольная фундаментальная последовательность в пространстве (X,ρ). Будем полагать, что это последовательность центров замкнутых шаров и покажем её сходимость, то есть полноту пространства (X,ρ). Выделим из последовательности {x_n} подпоследовательность {x_nk}, такую, что 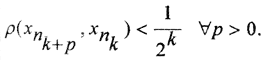Покажем, что подпоследовательность замкнутых шаров 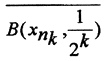является последовательностью вложенных шаров, т.е. 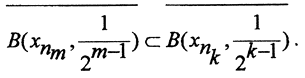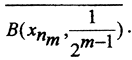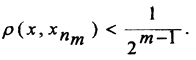при m>k Действительно, пусть произвольная точка х принадлежит шару Тогда Из неравенства треугольника найдём, что 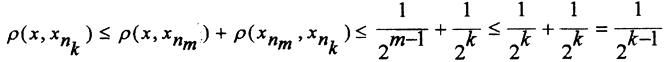Таким образом, точка х принадлежит и шару 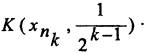Стало быть, шары вложены друг в друга. По условию теоремы последовательность вложенных шаров имеет непустое пересечение. Пусть x₀ - общая точка всех шаров. Поскольку радиусы вложенных шаров стремятся к нулю, то ρ(x₀,x_nk)_nk→∞→0 т.е. подпоследовательность {x_nk} сходится к точке x₀. Тогда и сама фундаментальная последовательность (x_n) сходится к той же точке x₀. Действительно, согласно неравенству треугольника имеем ρ(x₀,x_n)≤ρ(x₀,x_nk)+ρ(x_nk,x_n) При этом ρ(x₀,x_nk)→0 так как подпоследовательность {x_nk} сходится к x₀. Тогда ρ(x₀,x_n)→0, то есть последовательность {x_n} сходится.

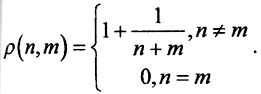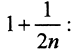
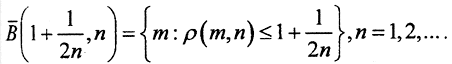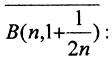
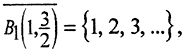
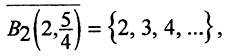
(Комментарий. Нарушение любых условий теоремы приводит к тому, что пересечение шаров пусто. Ранее было рассмотрено метрическое пространство (N,ρ), где N - множество натуральных чисел и Определим последовательность вложенных шаров с центром в точке n и радиуса Шары 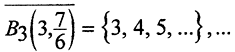замкнуты и вложены друг в друга, пространство (N,ρ) - полно, так как фундаментальные последовательности здесь могут быть только стационарными, а они сходятся. Но условие стремления к нулю радиусов шаров нарушено, поэтому пересечение вложенных шаров пусто: )

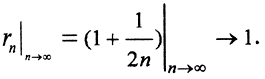Пример. Может ли в банаховом пространстве иметь пустое пересечение последовательность непустых вложенных замкнутых множеств?

Да, может. Рассмотрим банахово пространство вещественных чисел R и последовательность непустых замкнутых вложенных множеств в нем x_i = [i,∞), i=1,∞. Ясно, что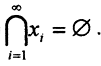

Определение 1. Пусть множество M⊂X, где X - носитель метрического пространства (X,ρ). Множество M⊂X называется множеством I категории, если его можно представить в виде объединения не более, чем счётного числа нигде не плотных множеств. Остальные множества называются множествами II категории.

Пример. Множество рациональных чисел есть множество I категории.

Теорема 2 (Теорема Бэра о категориях). Носитель X полного метрического пространства (X,ρ) есть множество II категории.

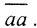
Пусть носитель X полного метрического пространства есть множество I-й категории, то есть 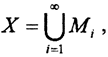, где M_i - нигде неплотные в пространстве (X,ρ) множества, а B₀ - некоторый замкнутый шар единичного радиуса. Так как M₁ нигде не плотное множество, оно не плотно и в B₀, то есть существует замкнутый шар B₁ радиуса менее 2^-1 такой, что B₁⊂ B₀ и B₁∩M₁. Поскольку множество M₂ нигде не плотно, то существует замкнутый шар B₂ радиусом менее 2^-2, для которого B₂∩M₂ = ∅. И так далее. В результате образуется последовательность вложенных замкнутых шаров 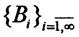полного метрического пространства (X,ρ), радиусы которых стремятся к нулю. Тогда по теореме 1 существует точка x∈X, принадлежащая всем шарам сразу. Но по построению B_i∩M_i = ∅, то есть x∉X, следовательно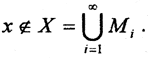

(Комментарий. Ясно, что в полном метрическом пространстве всякое не пустое открытое множество есть множество второй категории, а множества, дополнительные к множествам первой категории, тоже множества второй категории.)

Определение 2. Полное метрическое пространство (Y,ρ_y) называется пополнением метрического пространства (X,ρ_x), если пространство (X,ρ_x) всюду плотно в пространстве (Y,ρ_y).

Определение 3. Пространства (X,ρ_x) и (Y,ρ_y) называют изомерными, если между ними существует хоть одна биекция и ρ_y = ρ_x.

Теорема 3 (Теорема Хаусдорфа о пополнении метрических пространств). Любое неполное метрическое пространство (X,ρ_x) имеет единственное с точностью до изомерности пополнение.

1. Из элементов данного неполного метрического пространства (X,ρ_x) построим некоторое пространство (Y,ρ_y).

Фундаментальные последовательности {x_n} и {x'_n} метрического пространства (X,ρ) назовём конфинальными, если 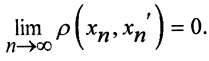Конфинальность определяет отношение эквивалентности x_n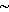x'_n, то есть это отношение рефлексивно, симметрично и транзитивно. Рефлексивность и симметричность очевидны, а из неравенства треугольника следует транзитивность. Действительно, пусть x_nx'_n, а x'_nx''_n. Тогда ρ(x_n,x''_n)≤ρ(x_n,x'_n)+ρ(x'_n,x''_n). Если ρ(x_n,x'_n)→0 и ρ(x'_n,x''_n)→0, то ρ(x_n,x''_n)→0. Отношение эквивалентности разбивает фундаментальные последовательности пространства (X,ρ_x) на непересекающиеся классы эквивалентных между собой последовательностей. Таким образом мы получили новое фактор-множество Y, элементами которого являются непересекающиеся классы фундаментальных последовательностей {α_n}, {β_n}, {γ_n},..., представителями которых являются фундаментальные последовательности {x_n}, {y_n}, {z_n},... пространства (X,ρ_x). Если фундаментальная последовательность {x_n} сходится к точке x, то и эквивалентная ей последовательность {α_n} сходится к той же точке. Действительно, пусть ρ(x_n,x)|_n→∞→0. Тогда ρ(α_n,x)≤ρ(α_n,x_n)+ρ(x_n,x)→0 и ρ(α_n,x)|_n→∞→0. Будем рассматривать фактор-множество Y как носитель нового метрического пространства (Y,ρ_y) с метрикой 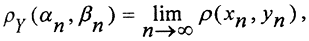, если, конечно, удастся доказать, что это метрика.

2. Покажем, что (Y,ρ_y) - метрическое пространство. Это значит, что предел 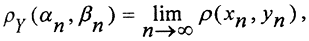существует, не зависит от выбора представителей и удовлетворяет аксиомам метрики.

2.1. Существование. Достаточно показать, что последовательность {ρ_n(x_n,y_n)} фундаментальна, тогда, в силу полноты числовой оси, она сходится. Полнота числовой оси доказывается независимо.

Лемма 1 (О четырёх точках). Для любых четырёх точек x,x',y,y' метрического пространства Х справедливо неравенство |ρ(x,y)-ρ(x',y')|≤ρ(x,x')+ρ(y,y').

ρ(x,y)≤ρ(x,x')+ρ(x',y)≤ρ(x,x')+ρ(x',y')+ρ(y',y) ⇒ ρ(x,y)-ρ(x',y')≤ρ(x,x')+ρ(y,y'). Поменяв местами x,y и x',y', получим ρ(x',y')-ρ(x,y)≤ρ(x',x)+ρ(y',y).

Отсюда сразу |ρ(x,y)-ρ(x',y')|≤ρ(x,x')+ρ(y,y').

Лемма 2 (О непрерывности метрики). Метрика ρ(x,y) является непрерывной функцией своих аргументов.

Из леммы 1 |ρ(x_n,y_n)-ρ(x,y)|≤ρ(x_n,x)+ρ(y_n,y)→0 при n→∞, то есть если ρ(x_n,x)→0 и ρ(y_n,y)→0 при n→∞, то ρ(x_n,y_n)→ρ(x,y).

Доказательство существования метрического пространства (Y,ρ_y).

Если последовательности {x_n} и {y_n} фундаментальные, то ρ(x_n,x_m)→0 и ρ(y_n,y_m)→0 при m,n→∞. Тогда согласно лемме о четырёх точках можно записать соотношение: |ρ(x_n,y_n)-ρ(x_m,y_m)|≤ρ(x_n,x_m)+ρ(y_n,y_m)→0 при m,n→∞. То есть числовая последовательность {ρ_n(x_n,y_n)} фундаментальна и, следовательно, и сходится в полном пространстве R¹₁.

2.2. Доказательство независимости от выбора представителей.

Пусть {x'_n}, {y'_n} - другие представители последовательностей {α_n}, {β_n}. Тогда |ρ(x_n,y_n)-ρ(x'_n,y'_n)|≤ρ(x_n,x'_n)+ρ(y_n,y'_n)→0. Так как последовательности {x_n}, {y_n} и {x'_n}, {y'_n} конфинальны, то ρ(x_n,x'_n)→0, ρ(y_n,y'_n)→0 и |ρ(x_n,y_n)-ρ(x'_n,y'_n)|→0.

2.3. Проверим выполнение аксиом метрики.

1. По свойствам пределов, связанных с неравенствами, если все члены последовательности {ρ_n(x_n,y_n)}≥0, то и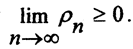

2. Симметричность очевидна.

3. Докажем аксиому треугольника. Так как ∀ n ρ(x_n,y_n)≤ρ(x_n,z_n)+ρ(z_n,y_n), то, по свойствам пределов, связанных с неравенствами и непрерывности метрики сразу получаем что и третья аксиома справедлива. Таким образом, пространство (Y,ρ_y) метрическое.

3. Покажем, что метрическое пространство (Y,ρ_y) и есть пополнение метрического пространства (X,ρ_x).

Надо показать, что: метрическое пространство (X,ρ_x) всюду плотно в метрическом пространстве (Y,ρ_y) и эти пространства изомерны.

3.1. Покажем, что метрическое пространство (X,ρ_x) всюду плотно в метрическом пространстве (Y,ρ_y).

Рассмотрим множество X' всех стационарных последовательностей пространства X. Все они одновременно являются и стационарными последовательностями в пространстве Y, то есть образуют подмножество Y'⊂Y, элементами которого являются стационарные последовательности. Обратное неверно. Таким образом,∀x,y∈X'ρ_X'(x,y) = ρ_Y'(α,β). Но любая стационарная последовательность из пространства Y'⊂Y принадлежит классу конфинальных последовательностей из пространства X, то есть ρ_X(x,y) = ρ_Y(α,β). Это значит, что пространство (X,ρ_x) изомерно вложено в пространство (Y',ρ_y). Осталось показать, что пространство и соответственно пространство Y' всюду плотно в пространстве Y. То есть каждый элемент α∈Y есть точка прикосновения множества Y' (и соответственно пространство X). Или в любой окрестности точки α∈Y найдётся точка α'∈Y'. Пусть {x_n}∈α∈Y - фундаментальная последовательность, то есть 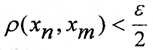при n,m>N. Зафиксировав m, получим, что {x_m} = α'∈Y' - стационарная последовательность. Расстояние между точками α∈Y и α'∈Y' в этом случае: 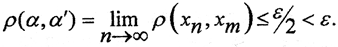Это значит, что в любой окрестности точки α∈Y найдётся точка α'∈Y', то есть пространство (Y',ρ_y) и, следовательно, пространство (X,ρ_X) всюду плотно в (Y,ρ_y).

3.2. Покажем, что метрическое пространство (Y,ρ_y) полно.

Рассмотрим некоторую фундаментальную последовательность {α_n}∈Y. Так как пространство (X,ρ_X) всюду плотно в (Y,ρ_y), то для каждого номера n найдётся элемент x_n∈X такой, что 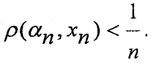Тогда из неравенства треугольника следует соотношение ρ(x_n,x_m)≤ρ(x_n,α_n)+ρα_n,x_m)<ε Это значит, что последовательность {x_n} фундаментальна и существует класс эквивалентности α₀, куда сходится последовательность {x_n}. Но тогда ρ_y(α₀,α_n)≤ρ_y(α₀,x_n)+ρ_y(x₀,α_n) и пределы существуют в силу полноты пространства R¹₁, то есть 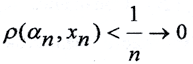ρ_y(α₀,x_n)→0. Таким образом, метрическое пространство (Y,ρ_Y) полно.

3.3. Покажем, что метрическое пространство (Y,ρ_Y) является единственным с точностью до изоморфизма пополнением метрического пространства (X,ρ_X).

Пусть (Y,ρ_Y) и (Y',ρ_Y) - два различных пополнения метрического пространства (X,ρ_X) и y₀∈Y - произвольная точка. Тогда ∃{x_n}∈X:{x_n}→y₀∈Y. Но, с другой стороны, {x_n}→y'₀∈Y', причём ρ(y₀,y'₀)≠0, а ρ(y₀,y'₀) = ρ(x_n,x_n)|_n→∞ = 0.